题目内容
13.若二项式(x+$\frac{1}{\sqrt{x}}$)6的展开式中的x3项大于15,且x为等比数列an的公比,则$\underset{lim}{n→∞}\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{{a}_{3}+{a}_{4}+…+{a}_{n}}$=1.分析 Tr+1=${∁}_{6}^{r}$x6-r$(\frac{1}{\sqrt{x}})^{r}$=${∁}_{6}^{r}$${x}^{6-\frac{3r}{2}}$,令$6-\frac{3r}{2}$=3,解得r.由${∁}_{6}^{2}$x3>15,解得x>1.再利用等比数列的前n项和公式、极限运算性质即可得出.
解答 解:Tr+1=${∁}_{6}^{r}$x6-r$(\frac{1}{\sqrt{x}})^{r}$=${∁}_{6}^{r}$${x}^{6-\frac{3r}{2}}$,
令$6-\frac{3r}{2}$=3,解得r=2.
T3=${∁}_{6}^{2}$x3,
∴${∁}_{6}^{2}$x3>15,解得x>1.
∵x为等比数列an的公比,
∴a1+a2+…+an=$\frac{{a}_{1}({x}^{n}-1)}{x-1}$,a3+a4+…+an=$\frac{{a}_{1}{x}^{2}({x}^{n-2}-1)}{x-1}$,
则$\underset{lim}{n→∞}\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{{a}_{3}+{a}_{4}+…+{a}_{n}}$=$\underset{lim}{n→∞}$$\frac{{x}^{n}-1}{{x}^{n}-{x}^{2}}$=$\underset{lim}{n→∞}$$\frac{1-\frac{1}{{x}^{n}}}{1-\frac{{x}^{2}}{{x}^{n}}}$=1.
故答案为:1.
点评 本题考查了二项式定理的应用、等比数列的前n项和公式、极限运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)=sin(2x+φ)在x=$\frac{π}{6}$处取得极大值,则函数y=f($\frac{π}{4}$+x)的图象( )
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
5.已知函数f(x)=ex,g(x)=x+1,则关于f(x),g(x)的语句为假命题的是( )
| A. | ?x∈R,f(x)>g(x) | B. | ?x1,x2∈R,f(x1)<g(x2) | ||
| C. | ?x0∈R,f(x0)=g(x0) | D. | ?x0∈R,使得?x∈R,f(x0)-g(x0)≤f(x)-g(x) |
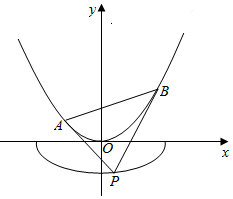 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.