题目内容
10.已知双曲线$\frac{x^2}{3}-{y^2}=1$的左右焦点分别为F1,F2,P为双曲线右支上一点,点Q的坐标为(-2,3),则|PQ|+|PF1|的最小值为5+$2\sqrt{3}$.分析 由双曲线方程求出a及c的值,利用双曲线定义把|PQ|+|PF1|转化为|PQ|+|PF2|+$2\sqrt{3}$,连接QF2交双曲线右支于P,则此时|PQ|+|PF2|最小等于|QF2|,由两点间的距离公式求出|QF2|,则|PQ|+|PF1|的最小值可求.
解答 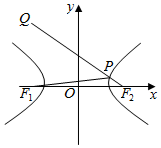 解:如图
解:如图
由双曲线$\frac{x^2}{3}-{y^2}=1$,得a2=3,b2=1,
∴c2=a2+b2=4,则c=2,
则F2(2,0),
∵$|P{F}_{1}|-|P{F}_{2}|=2\sqrt{3}$,∴$|P{F}_{1}|=2\sqrt{3}+|P{F}_{2}|$,
则|PQ|+|PF1|=|PQ|+|PF2|+$2\sqrt{3}$,
连接QF2交双曲线右支于P,
则此时|PQ|+|PF2|最小等于|QF2|,
∵Q的坐标为(-2,3),F2(2,0),
∴$|Q{F}_{2}|=\sqrt{(-2-2)^{2}+(3-0)^{2}}=5$,
∴|PQ|+|PF1|的最小值为5+$2\sqrt{3}$.
故答案为:5+$2\sqrt{3}$.
点评 本题考查双曲线的标准方程,考查了双曲线的简单性质,训练了双曲线中最值问题的求法,体现了数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知函数f(x)=ex,g(x)=x+1,则关于f(x),g(x)的语句为假命题的是( )
| A. | ?x∈R,f(x)>g(x) | B. | ?x1,x2∈R,f(x1)<g(x2) | ||
| C. | ?x0∈R,f(x0)=g(x0) | D. | ?x0∈R,使得?x∈R,f(x0)-g(x0)≤f(x)-g(x) |