题目内容
8.已知椭圆具有如下性质:若椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),则椭圆在其上一点A(x0,y0)处的切线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1,试运用该性质解决以下问题:椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其焦距为2,且过点$(1,\frac{{\sqrt{2}}}{2})$.点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,则△OCD面积的最小值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 依题意得:椭圆的焦点为F1(-1,0),F2(1,0),可得c=1,代入点$(1,\frac{{\sqrt{2}}}{2})$,计算即可求出a,b,从而可求椭圆C1的方程;设B(x2,y2),求得椭圆C1在点B处的切线方程,分别令x=0,y=0,求得截距,由三角形的面积公式,再结合基本不等式,即可求△OCD面积的最小值.
解答 解:由题意可得2c=2,即c=1,a2-b2=1,
代入点$(1,\frac{{\sqrt{2}}}{2})$,可得$\frac{1}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1,
解得a=$\sqrt{2}$,b=1,
即有椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1,
设B(x2,y2),
则椭圆C1在点B处的切线方程为$\frac{{x}_{2}}{2}$x+y2y=1
令x=0,yD=$\frac{1}{{y}_{2}}$,令y=0,可得xC=$\frac{2}{{x}_{2}}$,
所以S△OCD=$\frac{1}{2}$•$\frac{1}{{y}_{2}}$•$\frac{2}{{x}_{2}}$=$\frac{1}{{x}_{2}{y}_{2}}$,
又点B在椭圆的第一象限上,
所以x2,y2>0,$\frac{{{x}_{2}}^{2}}{2}$+y22=1,
即有$\frac{1}{{x}_{2}{y}_{2}}$=$\frac{\frac{{{x}_{2}}^{2}}{2}+{{y}_{2}}^{2}}{{x}_{2}{y}_{2}}$=$\frac{{x}_{2}}{2{y}_{2}}$+$\frac{{y}_{2}}{{x}_{2}}$≥2$\sqrt{\frac{{x}_{2}}{2{y}_{2}}•\frac{{y}_{2}}{{x}_{2}}}$=$\sqrt{2}$,
S△OCD≥$\sqrt{2}$,当且仅当$\frac{{{x}_{2}}^{2}}{2}$=y22=$\frac{1}{2}$,
所以当B(1,$\frac{\sqrt{2}}{2}$)时,三角形OCD的面积的最小值为$\sqrt{2}$.
故选:B.
点评 本题考查椭圆的方程的求法,考查三角形面积的最值的求法,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=0 | B. | $\overrightarrow{AB}$-$\overrightarrow{AD}$=0 | C. | ABCD为矩形 | D. | ABCD为菱形 |
| A. | e=-1 | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{a+b}{2}$ | B. | ab | C. | 2$\sqrt{ab}$ | D. | $\frac{{a}^{2}+{b}^{2}}{2}$ |
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,离心率为$\frac{1}{2}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长为4,离心率为$\frac{1}{2}$. 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其左、右焦点分别为F1(-c,0),F2(c,0)(c>0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其左、右焦点分别为F1(-c,0),F2(c,0)(c>0).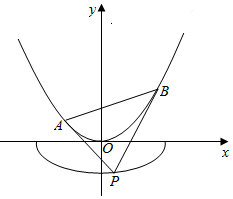 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.