题目内容
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)的极大值点有( )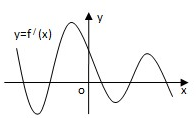

| A、1个 | B、2个 | C、3个 | D、4个 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:结合图象,根据导数大于零,即导函数的图象在x轴上方,说明原函数在该区间上是单调递增,否则为减函数,极大值点两侧导数的符号,从左往右,先正后负,因此根据图象即可求得极大值点的个数.
解答:
解:结合函数图象,根据极大值的定义可知在该点处从左向右导数符号先正后负,
从图象上可看出符合条件的有3点,
故选C.
从图象上可看出符合条件的有3点,
故选C.
点评:本题主要考查函数在某点取得极值的条件,以及学生的识图能力.属于基础题.

练习册系列答案
相关题目
设P是椭圆
+
=1上一点,F1,F2是椭圆的两个焦点,
•
=0,则△F1PF2面积是( )
| x2 |
| 25 |
| y2 |
| 5 |
| PF1 |
| PF2 |
| A、5 | B、10 | C、8 | D、9 |
已知等比数列{an}的前n项和为Sn,且满足
=5,则公比q=( )
| S4 |
| S2 |
A、±
| ||
B、
| ||
| C、±2 | ||
| D、2 |
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
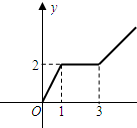
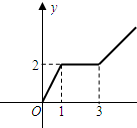
| A、-3 | B、-2 | C、-1 | D、2 |
已知直线l:y=x+m(m∈R),若以点M(2,0)为圆心的圆与直线l相切于点P,且P在y轴上,则该圆的方程为( )
| A、(x-2)2+y2=8 |
| B、(x+2)2+y2=8 |
| C、x2+(y-2)2=8 |
| D、x2+(y+2)2=8 |
已知某程序框图如图所示,则执行该程序后输出的结果是( )


| A、-1 | ||
B、
| ||
| C、2 | ||
| D、1 |
关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),且x12-x22=15,则实数a=( )
A、
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|