题目内容
关于x的不等式x2-2ax-8a2<0的解集为(x1,x2),且x12-x22=15,则实数a=( )
A、
| ||||||||
B、-
| ||||||||
C、-
| ||||||||
D、-
|
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据跟与系数的关系,得到关于a的方程解得即可,
解答:
解:∵x2-2ax-8a2<0的解集为(x1,x2),
∴x1,x2为方程x2-2ax-8a2=0,
∴x1+x2=2a,x1x2=-8a2,
又x12-x22=15,
∴(x12-x22)2=225,
∴[(x1+x2)2-2x1x2]2-4(x1x2)2=225,
∴144a4=225
∴a2=
∴a=±
,
故选:C.
∴x1,x2为方程x2-2ax-8a2=0,
∴x1+x2=2a,x1x2=-8a2,
又x12-x22=15,
∴(x12-x22)2=225,
∴[(x1+x2)2-2x1x2]2-4(x1x2)2=225,
∴144a4=225
∴a2=
| 5 |
| 4 |
∴a=±
| ||
| 2 |
故选:C.
点评:本题主要考查了一元二次方程根与系数的关系,培养了学生的转化能力,属于基础题.

练习册系列答案
相关题目
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)的极大值点有( )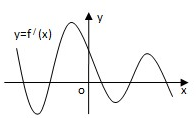

| A、1个 | B、2个 | C、3个 | D、4个 |
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相交,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,3) | ||||
B、(
| ||||
C、(1,
| ||||
| D、(3,+∞) |
在△ABC中,a=2,b=
,c=30°,则△ABC的面积是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线C:
-
=1(a>0,b>0)的一条渐近方程为y=
x,则C的离心率为( )
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|