题目内容
已知直线l:y=x+m(m∈R),若以点M(2,0)为圆心的圆与直线l相切于点P,且P在y轴上,则该圆的方程为( )
| A、(x-2)2+y2=8 |
| B、(x+2)2+y2=8 |
| C、x2+(y-2)2=8 |
| D、x2+(y+2)2=8 |
考点:圆的标准方程
专题:直线与圆
分析:由题意可得,点P的坐标为(0,m),再根据圆的半径MP即点M到直线l的距离,求得m的值,可得半径,从而得到圆的标准方程.
解答:
解:由题意可得,点P的坐标为(0,m),圆的半径MP即点M到直线l的距离,
∴
=
,求得 m=2,故半径为MP=2
,
故圆的方程为 (x-2)2+y2=8,
故选:A.
∴
| (2-0)2+(0-m)2 |
| |2-0+m| | ||
|
| 2 |
故圆的方程为 (x-2)2+y2=8,
故选:A.
点评:本题主要考查求圆的标准方程,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
设a,b,c∈R,且a>b,则( )
| A、a2>b2 | ||||
B、
| ||||
| C、lga>lgb | ||||
| D、2-a<2-b |
对于曲线y=ae
,令μ=lny,c=lna,v=
,可变换为线性回归模型,其形式为( )
| b |
| x |
| 1 |
| x |
| A、y=a+bv |
| B、μ=a+bv |
| C、μ=c+bv |
| D、y=c+bx |
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)的极大值点有( )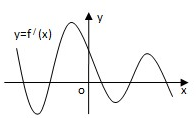

| A、1个 | B、2个 | C、3个 | D、4个 |
已知f(x)=
,则f(5)=( )
| x+2 |
| x-6 |
| A、-8 | B、-7 | C、-6 | D、-5 |
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相交,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,3) | ||||
B、(
| ||||
C、(1,
| ||||
| D、(3,+∞) |
已知双曲线C:
-
=1(a>0,b>0)的一条渐近方程为y=
x,则C的离心率为( )
| y2 |
| a2 |
| x2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
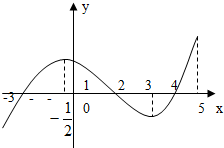 如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断:
如果函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列判断: