题目内容
设P是椭圆
+
=1上一点，F1，F2是椭圆的两个焦点，
•
=0，则△F1PF2面积是（ ）
| x2 |
| 25 |
| y2 |
| 5 |
| PF1 |
| PF2 |
| A、5 | B、10 | C、8 | D、9 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：在△PF1F2中，|PF1|=m，|PF2|=n，则m+n=10①，由勾股定理得80=m2+n2，②求出mn，即可求出△PF1F2的面积．
解答：
解：在△PF1F2中，|PF1|=m，|PF2|=n，则m+n=10①，
由勾股定理得80=m2+n2，②
①2-②，可得mn=10，
∴S△PF1F2=
mn=5．
故选：A．
由勾股定理得80=m2+n2，②
①2-②，可得mn=10，
∴S△PF1F2=
| 1 |
| 2 |
故选：A．
点评：本题考查椭圆的定义，考查勾股定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数y=f（x）对任意的实数x都有
=
+1，且f（1）=1，则f（2013）=（ ）
| 1 |
| f(x+2) |
| 1 |
| f(x+1) |
A、
| ||
B、
| ||
| C、2013 | ||
| D、2014 |
设a，b，c∈R，且a＞b，则（ ）
| A、a2＞b2 | ||||
B、
| ||||
| C、lga＞lgb | ||||
| D、2-a＜2-b |
已知函数f（x）是定义在实数集R上的不恒为零的偶函数，且对任意实数x都有xf（x+1）=（1+x）f（x），则f(
)的值是（ ）
| 2013 |
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
函数f（x）的定义域为R，导函数f′（x）的图象如图所示，则函数f（x）的极大值点有（ ）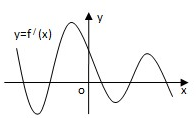
| A、1个 | B、2个 | C、3个 | D、4个 |