题目内容
已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(-2)=( )
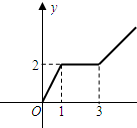
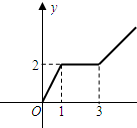
| A、-3 | B、-2 | C、-1 | D、2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质结合函数图象即可得到结论.
解答:
解:∵函数f(x)是定义在R上的奇函数,
∴f(-2)=-f(2)=-2,
故选:B
∴f(-2)=-f(2)=-2,
故选:B
点评:本题主要考查函数值的计算,根据函数的奇偶性以及函数图象进行转化时解决本题的关键.

练习册系列答案
相关题目
已知函数y=f(x)对任意的实数x都有
=
+1,且f(1)=1,则f(2013)=( )
| 1 |
| f(x+2) |
| 1 |
| f(x+1) |
A、
| ||
B、
| ||
| C、2013 | ||
| D、2014 |
已知函数f(x)是定义在实数集R上的不恒为零的偶函数,且对任意实数x都有xf(x+1)=(1+x)f(x),则f(
)的值是( )
| 2013 |
| 2 |
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |
已知三次函数f(x)=
x3-(4m-1)x2+(15m2-2m-7)x+2在x∈(-∞,+∞)是增函数,则m的取值范围是( )
| 1 |
| 3 |
| A、m<2或m>4 |
| B、2≤m≤4 |
| C、2<m<4 |
| D、-4<m<-2 |
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)的极大值点有( )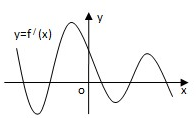

| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,a=2,b=
,c=30°,则△ABC的面积是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知奇函数f(x)当x>0时,f(x)=x(1-x),则当x<0时,f(x)的表达式是( )
| A、x(1+x) |
| B、-x(1-x) |
| C、-x(1+x) |
| D、x(x-1) |