题目内容
已知函数f(x)是定义在R上的偶函数,对于任意x∈R都f(x+6)=f(x)+f(3)成立;当x1,x2∈[0,3],且x1≠x2时,都有
>0.给出下列四个命题:
①f(3)=0;
②直线x=-6是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-9,-6]上为增函数;
④函数y=f(x)在[0,2014]上有335个零点.
其中正确命题的序号为 .
| f(x1)-f(x2) |
| x1-x2 |
①f(3)=0;
②直线x=-6是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-9,-6]上为增函数;
④函数y=f(x)在[0,2014]上有335个零点.
其中正确命题的序号为
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用
分析:①中,由题意,令x=-3,求出f(3)=0;
②中,由题意,求出f(x)的周期为6,且满足f(-6-x)=f(-6+x),得出x=-6是y=f(x)图象的对称轴;
③中,由题意,得出y=f(x)在[-3,0]上是减函数,从而得y=f(x)在[-9,-6]上的单调性;
④中,由题意,知y=f(x)在[0,6]上只有一个零点3,得出y=f(x)在[0,2014]上的零点数.
②中,由题意,求出f(x)的周期为6,且满足f(-6-x)=f(-6+x),得出x=-6是y=f(x)图象的对称轴;
③中,由题意,得出y=f(x)在[-3,0]上是减函数,从而得y=f(x)在[-9,-6]上的单调性;
④中,由题意,知y=f(x)在[0,6]上只有一个零点3,得出y=f(x)在[0,2014]上的零点数.
解答:
解:对于①,∵f(x+6)=f(x)+f(3),
∴f(-3+6)=f(-3)+f(3),
又∵f(-3)=f(3),
∴f(3)=f(3)+f(3),
∴f(3)=0,①正确;
对于②,由①知f(x+6)=f (x),∴f(x)的周期为6;
又∵f(x)是R上的偶函数,∴f(x+6)=f(-x);
而f(x)的周期为6,∴f(x+6)=f(-6+x),f(-x)=f(-x-6),
∴f(-6-x)=f(-6+x);
∴直线x=-6是y=f(x)图象的一条对称轴,②正确;
对于③,x1,x2∈[0,3],且x1≠x2时,有
>0,
即y=f(x)在[0,3]上是增函数;
∵f(x)是R上的偶函数,∴y=f(x)在[-3,0]上是减函数;
又f(x)的周期为6,∴y=f(x)在[-9,-6]上是减函数,③错误;
对于④,f(3)=0,且f(x)的周期为6,
又y=f(x)在[0,3]上为增函数,在[3,6]上为减函数,
∴y=f(x)在[0,6]上只有一个零点3,
又2014=335×6+3,
∴y=f(x)在[0,2014]上有335+1=336个零点,④错误.
综上,以上正确的命题是①②.
故答案为:①②.
∴f(-3+6)=f(-3)+f(3),
又∵f(-3)=f(3),
∴f(3)=f(3)+f(3),
∴f(3)=0,①正确;
对于②,由①知f(x+6)=f (x),∴f(x)的周期为6;
又∵f(x)是R上的偶函数,∴f(x+6)=f(-x);
而f(x)的周期为6,∴f(x+6)=f(-6+x),f(-x)=f(-x-6),
∴f(-6-x)=f(-6+x);
∴直线x=-6是y=f(x)图象的一条对称轴,②正确;
对于③,x1,x2∈[0,3],且x1≠x2时,有
| f(x1)-f(x2) |
| x1-x2 |
即y=f(x)在[0,3]上是增函数;
∵f(x)是R上的偶函数,∴y=f(x)在[-3,0]上是减函数;
又f(x)的周期为6,∴y=f(x)在[-9,-6]上是减函数,③错误;
对于④,f(3)=0,且f(x)的周期为6,
又y=f(x)在[0,3]上为增函数,在[3,6]上为减函数,
∴y=f(x)在[0,6]上只有一个零点3,
又2014=335×6+3,
∴y=f(x)在[0,2014]上有335+1=336个零点,④错误.
综上,以上正确的命题是①②.
故答案为:①②.
点评:本题考查了函数的单调性与奇偶性,周期性与对称性以及函数零点的综合应用问题,是较难的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
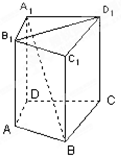 如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件
如图,在直四棱柱A1B1C1D1-ABCD中,当底面四边形ABCD满足条件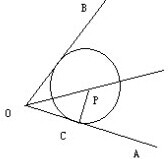 如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?
如图,点P是∠AOB平分线上一点,PC⊥OA,垂足为C,OB与以P为圆心、PC为半径的圆相切吗?为什么?