题目内容
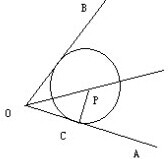如图，点P是∠AOB平分线上一点，PC⊥OA，垂足为C，OB与以P为圆心、PC为半径的圆相切吗？为什么？考点：圆的切线的性质定理的证明
专题：证明题,立体几何
分析：过P作PD⊥OB，交于D，由角平分线的性质定理和圆的切线的定义即可得到OB与以P为圆心、PC为半径的圆相切．
解答：
解：
OB与以P为圆心、PC为半径的圆相切．
理由如下：过P作PD⊥OB，交于D，
由于点P是∠AOB平分线上一点，PC⊥OA，
则PD=PC，
故由圆的切线的定义可得，
OB与以P为圆心、PC为半径的圆相切．
OB与以P为圆心、PC为半径的圆相切．理由如下：过P作PD⊥OB，交于D，
由于点P是∠AOB平分线上一点，PC⊥OA，
则PD=PC，
故由圆的切线的定义可得，
OB与以P为圆心、PC为半径的圆相切．
点评：本题考查圆的切线的性质和判定，考查角平分线的性质定理，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=（x-3）ex的单调递减区间是（ ）
| A、（-∞，2） |
| B、（0，3） |
| C、（1，4） |
| D、（2，+∞） |
如图，在三棱柱ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1⊥平面ABC，