题目内容
14.在数列{an}中,a1=2,(an+1-1)(an-1)+2an+1-2an=0(n∈N*),若an<$\frac{51}{50}$,则n的最小值为100.分析 令an-1=bn,确定$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=$\frac{1}{2}$,可得数列{$\frac{1}{{b}_{n}}$}是以1为首项,$\frac{1}{2}$为公差的等差数列,求出bn=$\frac{2}{n+1}$,可得an=$\frac{2}{n+1}$+1,利用an<$\frac{51}{50}$建立不等式,即可得出结论.
解答 解:令an-1=bn,则
∵(an+1-1)(an-1)+2an+1-2an=0,
∴bn+1bn+2bn+1-2bn=0
∴$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=$\frac{1}{2}$,
∵a1=2,∴$\frac{1}{{b}_{1}}$=1,
∴$\frac{1}{{b}_{n}}$=1+$\frac{1}{2}$(n-1)=$\frac{n+1}{2}$,
∴bn=$\frac{2}{n+1}$,
∴an-1=$\frac{2}{n+1}$,
∴an=$\frac{2}{n+1}$+1,
∵an<$\frac{51}{50}$,
∴$\frac{2}{n+1}$+1<$\frac{51}{50}$,
∴n>99,
∴n的最小值为100.
故答案为:100.
点评 本题考查数列递推式,考查等差数列的判定,考查学生的计算能力,正确转化是关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
6.若集合A={x|2x>1},集合B={x|lnx>0},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知函数y=2x2,则自变量从2变到2+△x函数值的增量△y为( )
| A. | 8 | B. | 8+2△x | C. | 2(△x)2+8△x | D. | 4△x+2(△x)2 |
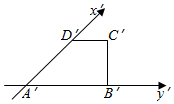 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.