题目内容
3.若函数f(x)=x${\;}^{\frac{1}{2}}$,则f(x)的反函数f-1(x)的定义域是[0,+∞).分析 由函数f(x)=x${\;}^{\frac{1}{2}}$≥0,即可得出f(x)的反函数f-1(x)的定义域.
解答 解:∵函数f(x)=x${\;}^{\frac{1}{2}}$≥0,则f(x)的反函数f-1(x)的定义域是[0,+∞).
故答案为:[0,+∞).
点评 本题考查了互为反函数的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
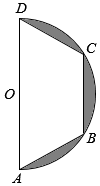 如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.
如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.