题目内容
9.设实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y≤10}\\{2x+y≥3}\\{0≤x≤4}\\{y≥1}\end{array}\right.$,则z=|x+y-10|的最大值是8.分析 作出不等式组对应的平面区域,利用点到直线的距离公式进行转化求解即可.
解答 解:作出不等式组对应的平面区域如图,
z=|x+y-10|=$\sqrt{2}$•$\frac{|x+y-10|}{\sqrt{2}}$,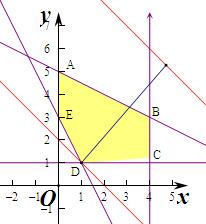
设d=$\frac{|x+y-10|}{\sqrt{2}}$,
则d的几何意义是区域内的点到直线x+y-10=0的距离,
则z=$\sqrt{2}$•d,
由图象知D到直线x+y-10=0的距离最大,
其中D(1,1),
此时d=$\frac{|1+1-10|}{\sqrt{2}}$=$\frac{8}{\sqrt{2}}$,
则z=$\sqrt{2}$•d=$\sqrt{2}$•$\frac{8}{\sqrt{2}}$=8,
故答案为:8,
点评 本题主要考查线性规划的应用,根据条件结合点到直线的距离公式进行转化是解决本题的关键.综合性较强.

练习册系列答案
相关题目
19.在三角形ABC中,已知AB=5,AC=7,AD是BC边上的中线,点E是AD的一个三等分点(靠近点A),则$\overrightarrow{AE}•\overrightarrow{BC}$=( )
| A. | 12 | B. | 6 | C. | 24 | D. | 4 |
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题: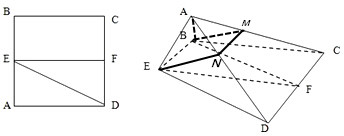 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.