题目内容
4.设a=${∫}_{0}^{\frac{π}{2}}$sinxdx,则(2x+$\frac{a}{x}$)6展开式的常数项为160.分析 由微积分基本定理可得a,再利用二项式定理的展开式的通项公式即可得出.
解答 解:a=${∫}_{0}^{\frac{π}{2}}$sinxdx=$(-cosx){|}_{0}^{\frac{π}{2}}$=1,
则(2x+$\frac{a}{x}$)6=$(2x+\frac{1}{x})^{6}$的展开式的通项公式:Tr+1=${∁}_{6}^{r}(2x)^{6-r}(\frac{1}{x})^{r}$=26-r${∁}_{6}^{r}$x6-2r,
令6-2r=0,解得r=3.
∴展开式的常数项为:23${∁}_{6}^{3}$=160.
故答案为:160.
点评 本题考查了微积分基本定理、二项式定理的展开式的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.下列函数中,既是奇函数又在R上单调递减的是( )
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x3 | D. | y=lnx |
12.若一个边长为a的正三角形,以其中一条高作为轴旋转,则所得旋转体的表面积为( )
| A. | $\frac{1}{4}$πa2 | B. | $\frac{1}{2}$πa2 | C. | $\frac{3}{4}$πa2 | D. | $\frac{1}{8}$πa2 |
19.在三角形ABC中,已知AB=5,AC=7,AD是BC边上的中线,点E是AD的一个三等分点(靠近点A),则$\overrightarrow{AE}•\overrightarrow{BC}$=( )
| A. | 12 | B. | 6 | C. | 24 | D. | 4 |
9.设集合M={x|y=$\sqrt{{{log}_2}x-1}$},N={x||x-1|≤2},则M∩N=( )
| A. | [2,+∞) | B. | [-1,3] | C. | [2,3] | D. | [-1,2] |
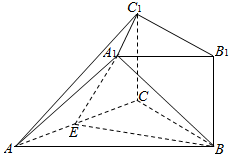 在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
在如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.