题目内容
2.已知数列{an}的前n项和Sn=$\frac{1}{2}$(n2+n),求数列{an}的通项公式.分析 由Sn,可得当n=1时,求出a1,当n≥2时,an=Sn-Sn-1,即可得出数列{an}的通项公式.
解答 解:∵Sn=$\frac{1}{2}$(n2+n),∴当n=1时,a1=$\frac{1}{2}$(1+1)=1,
当n≥2时,an=Sn-Sn-1=$\frac{1}{2}$(n2+n)-$\frac{1}{2}$[(n-1)2+(n-1)]=n.
当n=1时上式也成立,
∴an=n.
点评 本题考查了递推式的应用、等差数列的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
12.若一个边长为a的正三角形,以其中一条高作为轴旋转,则所得旋转体的表面积为( )
| A. | $\frac{1}{4}$πa2 | B. | $\frac{1}{2}$πa2 | C. | $\frac{3}{4}$πa2 | D. | $\frac{1}{8}$πa2 |
7.为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
| A. | y=sin($\frac{π}{30}$t+$\frac{π}{3}$) | B. | y=sin($\frac{π}{30}$t-$\frac{π}{3}$) | C. | y=sin(-$\frac{π}{30}$t+$\frac{π}{3}$) | D. | y=sin(-$\frac{π}{30}$t-$\frac{π}{3}$) |
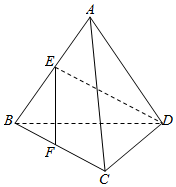 如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.
如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.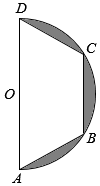 如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.
如图,等腰梯形ABCD,BC=$\frac{1}{2}$AD,将直径为4的半圆内的阴影部分以直径AD所在直线为轴,旋转一周得到一几何体,求该几何体的体积.