题目内容
定义在R上的奇函数f(x)满足f(x-2)=-f(x),且在[0,1]上是增函数,则有( )
A、f(
| ||||||
B、f(-
| ||||||
C、f(
| ||||||
D、f(-
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由已知分析出函数的周期性,结合函数的奇偶性和单调性,将三个自变量化为同一单调区间可比较得到答案.
解答:
解:定义在R上的奇函数f(x)图象必过原点(0,0),
又∵函数f(x)满足f(x-2)=-f(x),
∴f(x-4)=-f(x-2)=f(x),
∴函数f(x)是周期为4的周期函数,
∴f(
)=-f(-
)=f(
),
又∵函数f(x)在[0,1]上是增函数,
∴f(-
)=-f(
)<0<f(
)<f(
),
即f(-
)<f(
)<f(
)
故选B
又∵函数f(x)满足f(x-2)=-f(x),
∴f(x-4)=-f(x-2)=f(x),
∴函数f(x)是周期为4的周期函数,
∴f(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵函数f(x)在[0,1]上是增函数,
∴f(-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
即f(-
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
故选B
点评:本题考查的知识点是函数的奇偶性,函数的单调性,函数的周期性,是函数图象和性质的简单综合应用,难度中档.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
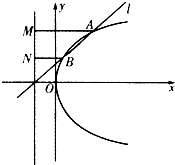 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
阅读如图所示的程序框图,运行相应的程序,输出的结果i=( )


| A、3 | B、4 | C、5 | D、6 |
(x-1)10的展开式中第6项系的系数是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知x,y满足
,则z=2x+y的最大值是( )
|
| A、1 | B、5 | C、7 | D、9 |