题目内容
已知函数f(x)=x2+a(x+lnx),x>0,a∈R是常数.试证明:
(1)?a∈R,y=(a+1)(2x-1)是函数y=f(x)的图象的一条切线;
(2)?a∈R,存在ξ∈(1,e),使f′(ξ)=
.
(1)?a∈R,y=(a+1)(2x-1)是函数y=f(x)的图象的一条切线;
(2)?a∈R,存在ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
考点:利用导数研究曲线上某点切线方程,特称命题
专题:导数的综合应用
分析:(1)求出原函数的导函数,求得y=(a+1)(2x-1)的斜率k=2(a+1),由导函数等于2(a+1)求得x的值,再求出f(1),由点斜式得直线方程,整理后证得答案;
(2)求出
的值,构造辅助函数g(x)=f′(ξ)-
,对a分类讨论,当a>e(e-1)2或a<
时,由函数零点存在定理证明,当
≤a≤e(e-1)2时,由均值不等式求出函数g(x)的最小值,而最小值小于0,进一步说明存在ξ∈(1,e),使g(ξ)=0,从而证得答案.
(2)求出
| f(e)-f(1) |
| e-1 |
| f(e)-f(1) |
| e-1 |
| (e-1)2 |
| e-2 |
| (e-1)2 |
| e-2 |
解答:
证明:(1)∵f(x)=x2+a(x+lnx),
∴f′(x)=2x+a(1+
),直线y=(a+1)(2x-1)的斜率k=2(a+1),
由2x+a(1+
)=2(a+1),得x=1,
∴f′(1)=2a+2,
又f(1)=1+a,
曲线y=f(x)在点(1,f(1))的切线为y-1-a=(2a+2)(x-1),
即y=(a+1)(2x-1),
∴y=(a+1)(2x-1)是曲线y=f(x)的一条切线;
(2)直接计算知
=e+1+a+
,
设函数g(x)=f′(x)-
=2x-(e+1)+
-
,
g(1)=1-e+a-
=
,
g(e)=e-1+
-
=
,
当a>e(e-1)2或a<
时,g(1)•g(e)=-
<0,
∵y=g(x)的图象是一条连续不断的曲线,∴存在ξ∈(1,e),使g(ξ)=0,
即ξ∈(1,e),使f′(ξ)=
;
当
≤a≤e(e-1)2时,g(1)、g(e)≥0,而且g(1)、g(e)之中至少一个为正,
由均值不等式知,g(x)≥2
-
,等号当且仅当x=
∈(1,e)时成立,
∴g(x)有最小值m=2
-
=
,
且m=
=
<0,
此时存在ξ∈(1,e)(ξ∈(1,
)或ξ∈(
,e)),使g(ξ)=0.
综上所述,?a∈R,存在ξ∈(1,e),使f′(ξ)=
.
∴f′(x)=2x+a(1+
| 1 |
| x |
由2x+a(1+
| 1 |
| x |
∴f′(1)=2a+2,
又f(1)=1+a,
曲线y=f(x)在点(1,f(1))的切线为y-1-a=(2a+2)(x-1),
即y=(a+1)(2x-1),
∴y=(a+1)(2x-1)是曲线y=f(x)的一条切线;
(2)直接计算知
| f(e)-f(1) |
| e-1 |
| a |
| e-1 |
设函数g(x)=f′(x)-
| f(e)-f(1) |
| e-1 |
| a |
| x |
| a |
| e-1 |
g(1)=1-e+a-
| a |
| e-1 |
| a(e-2)-(e-1)2 |
| e-1 |
g(e)=e-1+
| a |
| e |
| a |
| e-1 |
| e(e-1)2-a |
| e(e-1) |
当a>e(e-1)2或a<
| (e-1)2 |
| e-2 |
| [a(e-2)-(e-1)2]•[a-e(e-1)2] |
| e(e-1)2 |
∵y=g(x)的图象是一条连续不断的曲线,∴存在ξ∈(1,e),使g(ξ)=0,
即ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
当
| (e-1)2 |
| e-2 |
由均值不等式知,g(x)≥2
| 2a |
| a+e2-1 |
| e-1 |
|
∴g(x)有最小值m=2
| 2a |
| a+e2-1 |
| e-1 |
-a+2(e-1)
| ||
| e-1 |
且m=
-a+2(e-1)
| ||
| e-1 |
-[
| ||||
| e-1 |
此时存在ξ∈(1,e)(ξ∈(1,
|
|
综上所述,?a∈R,存在ξ∈(1,e),使f′(ξ)=
| f(e)-f(1) |
| e-1 |
点评:本题考查利用导数研究曲线上某点的切线方程,训练了函数构造法,考查了利用函数零点存在性定理判断函数零点的个数,体现了数学转化思想方法,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
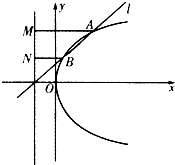 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
(x-1)10的展开式中第6项系的系数是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知x,y满足
,则z=2x+y的最大值是( )
|
| A、1 | B、5 | C、7 | D、9 |
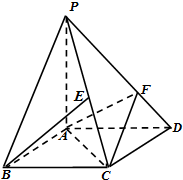 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,设E为PC中点,点F在线段PD上且PF=2FD. PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从360天的市区PM2.5监测数据中,随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).