题目内容
已知双曲线C:
-
=1(a>0,b>0)的焦距为2
,其一条渐近线的倾斜角为θ,且tanθ=
.以双曲线C的实轴为长轴,虚轴为短轴的椭圆记为E.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设点A是椭圆E的左顶点,P、Q为椭圆E上异于点A的两动点,若直线AP、AQ的斜率之积为-
,问直线PQ是否恒过定点?若恒过定点,求出该点坐标;若不恒过定点,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设点A是椭圆E的左顶点,P、Q为椭圆E上异于点A的两动点,若直线AP、AQ的斜率之积为-
| 1 |
| 4 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据双曲线的性质计算a,b,c.注意焦点在x轴上的渐近线方程为y=±
x.
(Ⅱ)当斜率存在时,设出直线方程y=kx+m,再联立椭圆方程和直线方程,设出两个交点P(x1,y1),Q(x2,y2),根据kAP•kAQ=-
,找出k和m的关系,从而求定点;当斜率不存在时单独讨论.
| b |
| a |
(Ⅱ)当斜率存在时,设出直线方程y=kx+m,再联立椭圆方程和直线方程,设出两个交点P(x1,y1),Q(x2,y2),根据kAP•kAQ=-
| 1 |
| 4 |
解答:
解:(Ⅰ)双曲线
-
=1的焦距2c=2
,则c=
,∴a2+b2=7,①
渐近线方程y=±
x,由题知tanθ=
=
,②
由①②解得a2=4,b2=3,
∴椭圆E的方程为
+
=1.
(Ⅱ)在(Ⅰ)的条件下,当直线PQ的斜率存在时,设直线PQ的方程为y=kx+m,
由
,消去y得:(3+4k2)x2+8kmx+4m2-12=0,
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1x2=
,
又A(-2,0),由题知kAP•kBQ=
•
=-
,
则(x1+2)(x2+2)+4y1y2=0,且x1,x2≠-2,
则x1•x2+2(x1+x2)+4+4(kx1+m)(kx2+m)
=(1+4k2)x1x2+(2+4km)(x1+x2)+4m2+4
=
+(2+4km)
+4m2+4=0
则m2-km-2k2=0,
∴(m-2k)(m+k)=0,
∴m=2k或m=-k.
当m=2k时,直线PQ的方程为y=kx+2k=k(x+2).
此时直线PQ过定点(-2,0),显然不适合题意.
当m=-k时,直线PQ的方程为y=kx-k=k(x-1),此时直线PQ过定点(1,0).
当直线PQ的斜率不存在时,若直线PQ过定点(1,0),P、Q点的坐标分别为(1,
),(1,-
),满足kAP•kAQ=-
.
综上,直线PQ过定点(1,0).
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 7 |
渐近线方程y=±
| b |
| a |
| b |
| a |
| ||
| 2 |
由①②解得a2=4,b2=3,
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)在(Ⅰ)的条件下,当直线PQ的斜率存在时,设直线PQ的方程为y=kx+m,
由
|
设P(x1,y1),Q(x2,y2),则x1+x2=
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
又A(-2,0),由题知kAP•kBQ=
| y1 |
| x1+2 |
| y2 |
| x2+2 |
| 1 |
| 4 |
则(x1+2)(x2+2)+4y1y2=0,且x1,x2≠-2,
则x1•x2+2(x1+x2)+4+4(kx1+m)(kx2+m)
=(1+4k2)x1x2+(2+4km)(x1+x2)+4m2+4
=
| (1+4k2)(4m2-12) |
| 3+4k2 |
| -8km |
| 3+4k2 |
则m2-km-2k2=0,
∴(m-2k)(m+k)=0,
∴m=2k或m=-k.
当m=2k时,直线PQ的方程为y=kx+2k=k(x+2).
此时直线PQ过定点(-2,0),显然不适合题意.
当m=-k时,直线PQ的方程为y=kx-k=k(x-1),此时直线PQ过定点(1,0).
当直线PQ的斜率不存在时,若直线PQ过定点(1,0),P、Q点的坐标分别为(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
综上,直线PQ过定点(1,0).
点评:本题是圆锥曲线和直线位置关系的常见类型,都是通过设而不求的方法,联立方程组,再由题目中给定的等式,寻求量与量之间的关系,从而求得定点.另外,直线的斜率是否存在也是需要讨论的情况.这在高考中是常考题型.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
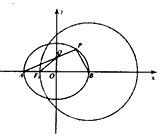 如图,点A,B分别是椭圆E:
如图,点A,B分别是椭圆E: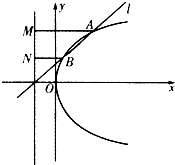 如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )
如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )