题目内容
若点（x，y）在曲线y=-|x|与y=-2所围成的封闭区域内（包括边界），则2x-y的最大值为（ ）
| A、-6 | B、4 | C、6 | D、8 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，设z=2x-y，利用z的几何意义，即可得到结论．
解答：
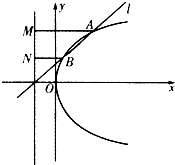
解：作出曲线y=-|x|与y=-2所围成的封闭区域内（包括边界）如图：
设z=2x-y，则y=2x-z，
平移直线y=2x-z，
由图象可知当直线y=2x-z经过点A时，直线y=2x-z的截距最小，此时z最大，
由
，解得
，
即A（2，-2），此时z=2×2-（-2）=4+2=6，
故选：C
设z=2x-y，则y=2x-z，
平移直线y=2x-z，
由图象可知当直线y=2x-z经过点A时，直线y=2x-z的截距最小，此时z最大，
由
|
|
即A（2，-2），此时z=2×2-（-2）=4+2=6，
故选：C
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
如图，点A，B分别是椭圆E：
执行如图所示的程序框图所表示的程序，则所得的结果为执行如图所示的程序框图，输入的N=2014，则输出的S=（ ）
| A、2011 | B、2012 |
| C、2013 | D、2014 |
如图，已知直线l：y=k（x+1）（k＞0）与抛物线C：y2=4x相交于A、B两点，且A、B两点在抛物线C准线上的射影分别是M、N，若|AM|=2|BN|，则k的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
（x-1）10的展开式中第6项系的系数是（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大．我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．某市环保局从360天的市区PM2.5监测数据中，随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．