题目内容

已知f（x）=
cx
2x+3
（c为常数），满足f[f（x）]=x．求f（x）．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由题意，求出f[f（x）]，利用函数恒等式列出方程组，求出c的值即得f（x）的解析式．
解答： 解：∵f（x）=
cx
2x+3
，
∴f[f（x）]=f[
cx
2x+3
]
=
c•
cx
2x+3
2•
cx
2x+3
+3

=
c2x
(2c+6)x+9
=x；
∴c2x=（2c+6）x2+9x，
即
2c+6=0
c2=9
，
解得c=-3；
∴f（x）=
-3x
2x+3
=-
3x
2x+3
．
点评：本题考查了求函数解析式的问题，解题的关键是表示出f[f（x）]，利用函数恒等式列出方程组，是基础题．
练习册系列答案
相关题目
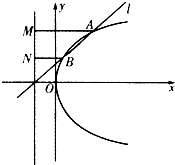如图，已知直线l：y=k（x+1）（k＞0）与抛物线C：y2=4x相交于A、B两点，且A、B两点在抛物线C准线上的射影分别是M、N，若|AM|=2|BN|，则k的值是（　　）
A、
1
3
B、
2
3
C、
2
3
2
D、2
2
已知椭圆C1的中心在坐标原点，两焦点分别为F1（-2，0），F2（2，0），点A（2，3）在椭圆C1上，又抛物线C2：x2=2py（p＞0）通径所在直线被椭圆C1所截得的线段长为
4
3
33

（1）求椭圆C1和抛物线C2的方程；
（2）过点A的直线L与抛物线C2交于B、C两点，抛物线C2在点B、C处的切线分别为l1、l2，且l1与l2交于点P．是否存在满足|PF1|+|PF2|=|AF1|+|AF2|的点P？若存在，指出这样的点P有几个（不必求出点P的坐标），若不存在，说明理由．
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，对人体健康和大气环境质量的影响很大．我国PM2.5标准采用世卫组织设定的最宽限值，即PM2.5日均值在35微克/立方以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．某市环保局从360天的市区PM2.5监测数据中，随机抽取15天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．
（1）从这15天的数据中任取3天的数据，记ξ表示空气质量达到一级的天数，求ξ的分布列；
（2）以这15天的PM2.5日均值来估计这360天的空气质量情况，则其中大约有多少天的空气质量达到一级．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，以原点为圆心，椭圆的短半轴长为半径的圆与直线x-y+
2
=0相切．
（1）求椭圆C的方程；
（2）若过点M（2，0）的直线与椭圆C相交于两点A，B，以OA，OB为邻边作一个平行四边形OAQB，记直线OQ与椭圆交于P点，且满足
|OQ|
|OP|
=λ（O为坐标原点），求实数λ的取值范围．
已知椭圆C的两个焦点是（0，-
3
）和（0，
3
），并且经过点(
3
2
 ，  1)，抛物线的顶点E在坐标原点，焦点恰好是椭圆C的右顶点F．
（Ⅰ）求椭圆C和抛物线E的标准方程；
（Ⅱ）过点F作两条斜率都存在且互相垂直的直线l1、l2，l1交抛物线E于点A、B，l2交抛物线E于点G、H，求
AG
•
HB
的最小值．
下列几个命题：
①函数f(x)=(
x
)2与g（x）=x表示的是同一个函数；
②若函数f（x）的定义域为[1，2]，则函数f（x+1）的定义域为[2，3]；
③若函数f（x）的值域是[1，2]，则函数f（x+1）的值域为[2，3]；
④若函数f（x）=x2+mx+1是偶函数，则函数f（x）的减区间为（-∞，0]．
其中正确的命题有
 
个．
已知函数f（x）=x2（ex+e-x）-（2x+1）2（e2x+1+e-2x-1），则满足f（x）＞0的实数x的取值范围为
 
．
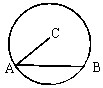
如图，在半径为R的圆C中，已知弦AB的长为5，则
AB
•
AC
=（　　）
A、
5
2
B、
25
2
C、
5
2
R
D、
25
2
R

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网