题目内容
设向量
=（cosα，sinα），
=（sinβ，cosβ），若
•
=-
，则＜
，
＞=（ ）
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、-30° |
| C、150° | D、120° |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的模的计算公式、向量的夹角公式即可得出．
解答：
解：∵
•
=-
，|
|=
=1，|
|=
=1．
∴cos＜
，
＞=
=-
，
∴＜
，
＞=120°．
故选：D．
| a |
| b |
| 1 |
| 2 |
| a |
| cos2α+sin2α |
| b |
| sin2β+cos2β |
∴cos＜
| a |
| b |
| ||||
|
|
| 1 |
| 2 |
∴＜
| a |
| b |
故选：D．
点评：本题考查了向量的模的计算公式、向量的夹角公式，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
812014除以100的余数是（ ）
| A、1 | B、79 | C、21 | D、81 |
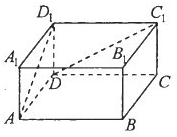如图，在长方体ABCD-A1B1C1D1中，底面是边长为2的正方形，高为1，则异面直线AD1和DC1所成角的余弦值等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
角α的终边过P（sin
，cos
），则角α的最小正值是（ ）
| 2π |
| 3 |
| 2π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中，若|
|=3，|
|=4，∠BAC=60°，则
•
=（ ）
| AB |
| AC |
| BA |
| AC |
| A、6 | B、4 | C、-6 | D、-4 |
双曲线
-
=1的渐近线方程是（ ）
| y2 |
| 9 |
| x2 |
| 16 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
已知函数y=sinx（x∈R）的图象如图所示，则t的值是（ ）
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示．