题目内容
812014除以100的余数是（ ）
| A、1 | B、79 | C、21 | D、81 |
考点：二项式定理的应用
专题：二项式定理
分析：利用二项式定理化简812014=（80+1）2014，求出展开式的后2项，即可得到812014除以100的余数是
解答：
解：812014=(80+1)2014=
8092+
8091+…
80+
=m•102+2014×80+1（m∈N）
=m•102+161120+14
即812014除以100的余数为21．
故选：C．
| C | 0 2014 |
| C | 1 2014 |
| C | 2013 2014 |
| C | 2014 2014 |
=m•102+2014×80+1（m∈N）
=m•102+161120+14
即812014除以100的余数为21．
故选：C．
点评：本题考查二项式定理的应用，注意二项式定理的展开式的后2项，易错题．
练习册系列答案
相关题目
已知命题P：?x∈（0，1），x2＜x3；命题q：若函数f（x）=ln（a+
）为奇函数，则a=-1，下列命题中真命题是（ ）
| 2 |
| x+1 |
| A、p∧q | B、p∧￢q |
| C、￢p∧q | D、￢p∧￢q |
下列四个函数中，能在x=0处取得极值的是（ ）
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x．
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x．
| A、①② | B、②③ | C、③④ | D、①③ |
如图，正方形ACDE与等腰直角三角形ACB所在的平面互相垂直，且AC=BC=2，∠ACB=90°，F，G分别是线段AE，BC的中点，则AD与GF所成的角的余弦值为（ ）A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若△ABC三内角A、B、C成等差数列，则∠B=60°的推理过程是（ ）
| A、归纳推理 | B、类比推理 |
| C、演绎推理 | D、合情推理 |
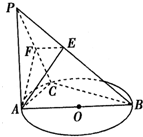如图，PA垂直于圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC，
正确命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
在区域D：（x-1）2+y2≤4内随机取一个点，则此点到点A（1，2）的距离小于2的概率是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
设向量
=（cosα，sinα），
=（sinβ，cosβ），若
•
=-
，则＜
，
＞=（ ）
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、-30° |
| C、150° | D、120° |