题目内容
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示．（1）求函数f（x）的解析式；
（2）求函数f（x）的单调增区间；
（3）若x∈[-
| 3π |
| 8 |
| π |
| 4 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）利用函数的图象求出A和函数的周期，求出ω，即可求函数f（x）的解析式；
（2）利用正弦函数的单调增区间直接求解函数f（x）的单调增区间；
（3）通过x∈[-
，
]，求出相位的范围，利用正弦函数的值域，求函数f（x）的值域．
（2）利用正弦函数的单调增区间直接求解函数f（x）的单调增区间；
（3）通过x∈[-
| 3π |
| 8 |
| π |
| 4 |
解答：
解：（1）由题意知：A=2，T=2×(
+
)=π，
∴ω=2--------------------（2分）
函数f（x）的解析式：f(x)=2sin(2x+
)--------------------（5分）
（2）由2kπ-
≤2x+
≤2kπ+
，k∈Z
得kπ-
≤x≤kπ-
--------------------（7分）
减区间为[kπ-
，kπ-
]，k∈Z--------------------（10分）
（3）∵x∈[-
，
]，
∴2x+
∈[0，
]，
∴2sin(2x+
)∈[-
，2]．
∴函数的值域为[-
，2]-------------------（16分）
| 3π |
| 8 |
| π |
| 8 |
∴ω=2--------------------（2分）
函数f（x）的解析式：f(x)=2sin(2x+
| 3π |
| 4 |
（2）由2kπ-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
得kπ-
| 5π |
| 8 |
| π |
| 8 |
减区间为[kπ-
| 5π |
| 8 |
| π |
| 8 |
（3）∵x∈[-
| 3π |
| 8 |
| π |
| 4 |
∴2x+
| 3π |
| 4 |
| 5π |
| 4 |
∴2sin(2x+
| 3π |
| 4 |
| 2 |
∴函数的值域为[-
| 2 |
点评：本题考查三角函数的解析式的求法，函数的单调性以及正弦函数的值域的求法，考查计算能力．
练习册系列答案
同步练习强化拓展系列答案
相关题目
设向量
=（cosα，sinα），
=（sinβ，cosβ），若
•
=-
，则＜
，
＞=（ ）
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、-30° |
| C、150° | D、120° |
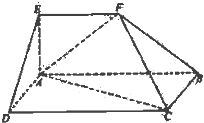在多面体ABCDEF中，四边形ABCD是矩形，在四边形ABFE中，AB∥EF，∠EAB=90°，AB=4，AD=AE=EF=2，平面ABFE⊥平面ABCD．