题目内容
马航MH370失踪牵动全球人的眼光,某卫星发现海上A处北偏东45°方向,距离A点100(
-1)海里的B处有一疑是漂浮物,在A处北偏西75°方向,距离A点200海里的C处我方“海巡1号”奉命以10
海里/小时的速度去捕捞此漂浮物,而漂浮物顺洋流正以10海里/小时的速度,以B处向北偏东30°方向漂流.问海巡1号沿什么方向行驶才能最快到达疑是漂浮物出,并求出所需时间.
| 3 |
| 3 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:设海巡1号用th在D处到达疑是漂浮物出,进而可表示出CD和BD,进而在△ABC中利用余弦定理求得BC,在△BCD中,根据正弦定理可求得sin∠BCD的值,进而求得∠BDC=∠BCD=30°,求得BD,再利用BD=100
求得t.
| 6 |
解答:
 解:如图所示:设海巡1号用th在D处到达疑是漂浮物出,
解:如图所示:设海巡1号用th在D处到达疑是漂浮物出,
则有CD=10
t,BD=10t.
在△ABC中,∵AB=100(
-1),AC=200,∠BAC=120°,
∴由余弦定理可得 BC2=AB2+AC2-2AB•AC•cos∠BAC
=[100(
-1)]2+2002-2×100(
-1)×200×cos120°=6,
∴BC=100
.
由正弦定理得sin∠ABC=
•sin∠BAC=
,解得∠ABC=45°,即BC与正北方向垂直.
于是∠CBD=120°.
在△BCD中,由正弦定理可得sin∠BCD=
=
,
∴∠BCD=30°,
∵∠CBD=120°,∴∠BCD=30°,∠BDC=30°,
∴BD=BC=100
,则有10t=100
,t=10
∴海巡1号沿北偏东60°方向,需10
小时才能最快到达疑是漂浮物出.
 解:如图所示:设海巡1号用th在D处到达疑是漂浮物出,
解:如图所示:设海巡1号用th在D处到达疑是漂浮物出,则有CD=10
| 3 |
在△ABC中,∵AB=100(
| 3 |
∴由余弦定理可得 BC2=AB2+AC2-2AB•AC•cos∠BAC
=[100(
| 3 |
| 3 |
∴BC=100
| 6 |
由正弦定理得sin∠ABC=
| AC |
| BC |
| ||
| 2 |
于是∠CBD=120°.
在△BCD中,由正弦定理可得sin∠BCD=
| BD•sin∠CBD |
| CD |
| 1 |
| 2 |
∴∠BCD=30°,
∵∠CBD=120°,∴∠BCD=30°,∠BDC=30°,
∴BD=BC=100
| 6 |
| 6 |
| 6 |
∴海巡1号沿北偏东60°方向,需10
| 6 |
点评:本题主要考查了解三角形的实际应用.考查了运用三角函数的基础知识解决实际的问题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
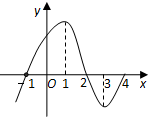 如图所示为y=f′(x)的图象,则下列判断正确的是( )
如图所示为y=f′(x)的图象,则下列判断正确的是( )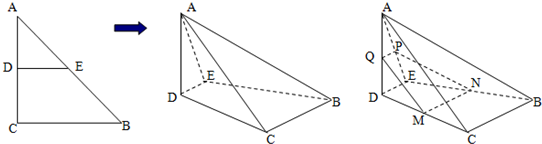
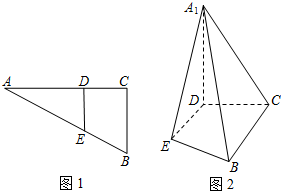 如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2)
如图1直角△ABC中,两直角边长分别是BC=3,AC=6,D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD(如图2) 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.