题目内容
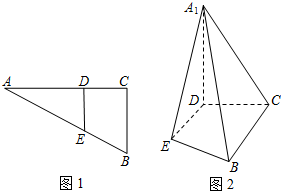如图1直角△ABC中，两直角边长分别是BC=3，AC=6，D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD（如图2）（Ⅰ）求证：A1D⊥EC；
（Ⅱ）判断如下两个两个命题的真假，并说明理由．
①BC∥平面A1DE
②EB∥平面A1DC．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：（I）利用线面垂直的判定与性质定理即可得出；
（II）①利用线面平行的判定定理即可得出；
②利用线面平行的判定与性质定理及其反证法即可得出．
（II）①利用线面平行的判定定理即可得出；
②利用线面平行的判定与性质定理及其反证法即可得出．
解答：
证明：（Ⅰ）在△ABC中，∠C=90°，DE∥BC，
∴AD⊥DE，∴A1D⊥DE．
又A1D⊥CD，CD∩DE=D，∴A1D⊥平面BCDE，
又EC?平面BCDE，∴A1D⊥EC．
（Ⅱ）命题①是真命题，证明如下：
∵DE∥BC，DE?平面A1DE，BC?平面A1DE，
∴BC∥平面A1DE．
命题②是假题
（反证法）若EB∥平面A1DC，又EB?平面BCDE，平面BCDE∩平面A1DC=CD，
据直线与平面平行的性质定理，EB∥DC，这与直角三角形矛盾，所以假设不成立，
故命题②是假命题．
∴AD⊥DE，∴A1D⊥DE．
又A1D⊥CD，CD∩DE=D，∴A1D⊥平面BCDE，
又EC?平面BCDE，∴A1D⊥EC．
（Ⅱ）命题①是真命题，证明如下：
∵DE∥BC，DE?平面A1DE，BC?平面A1DE，
∴BC∥平面A1DE．
命题②是假题
（反证法）若EB∥平面A1DC，又EB?平面BCDE，平面BCDE∩平面A1DC=CD，
据直线与平面平行的性质定理，EB∥DC，这与直角三角形矛盾，所以假设不成立，
故命题②是假命题．
点评：本题综合考查了线面垂直与平行的判定与性质定理及其反证法，考查了推理能力，属于难题．
练习册系列答案
相关题目
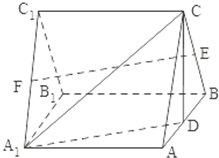如图，三棱柱ABC-A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等．D，E，F分别为棱AB，BC，A1C1的中点．