题目内容
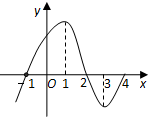如图所示为y=f′（x）的图象，则下列判断正确的是（ ）①f（x）在（-∞，1）上是增函数；
②x=-1是f（x）的极小值点；
③f（x）在（2，4）上是减函数，在（-1，2）上是增函数；
④x=2是f（x）的极小值点．
| A、①②③ | B、①③④ |
| C、③④ | D、②③ |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：通过图象，结合导函数的符号，逐一排除，从而选出正确选项．
解答：
解：x＜-1时，f′（x）＜0，∴f（x）是增函数，故①错误，②正确，
-1＜x＜2时，f′（x）＞0，f（x）是增函数，2＜x＜4时，f′（x）＜0，f（x）是减函数，故③正确，
x=2是极大值点，故④错误，
故选：D．
-1＜x＜2时，f′（x）＞0，f（x）是增函数，2＜x＜4时，f′（x）＜0，f（x）是减函数，故③正确，
x=2是极大值点，故④错误，
故选：D．
点评：本题考察了函数的单调性，导数的应用，读图的能力，是一道基础题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知m，n是两条不同的直线，α，β，γ是三个不同的平面，下列命题正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若α⊥β，α⊥γ，则β∥γ |
| C、若m∥α，m∥β，则α∥β |
| D、若m⊥α，m⊥β，则α∥β |
不等式sin（π+x）＞0成立的x的取值范围为（ ）
| A、（0，π） |
| B、（π，2π） |
| C、（2kπ，2kπ+π）（k∈Z） |
| D、（2kπ+π，2kπ+2π）（k∈Z） |
由直线y=0，x=e，y=2x及曲线y=
所围成的封闭的图形的面积为（ ）
| 2 |
| x |
| A、3 |
| B、3+2ln2 |
| C、e2-3 |
| D、e |
若复数z满足z=1-2i，则z的虚部为（ ）
| A、-2i | B、2i | C、-2 | D、2 |
已知f(x)=
，则函数g（x）=f（x）-ex的零点个数为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
若函数f（x）的零点与g（x）=lnx+2x-8的零点之差的绝对值不超过0.5，则f（x）可以是（ ）
| A、f（x）=3x-6 | ||
| B、f（x）=（x-4）2 | ||
| C、f（x）=ex-1-1 | ||
D、f（x）=ln（x-
|