题目内容
已知:如图,等腰直角三角形ABC的直角边AC=BC=2,沿其中位线DE将平面ADE折起,使平面ADE⊥平面BCDE,得到四棱锥A-BCDE,设CD、BE、AE、AD的中点分别为M、N、P、Q.
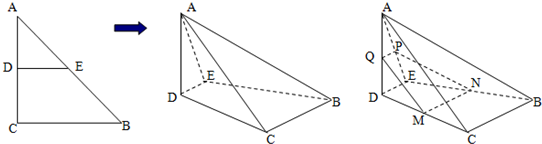
(1)求证:M、N、P、Q四点共面;
(2)求证:平面ABC⊥平面ACD;
(3)求异面直线BE与MQ所成的角.

(1)求证:M、N、P、Q四点共面;
(2)求证:平面ABC⊥平面ACD;
(3)求异面直线BE与MQ所成的角.
考点:平面与平面垂直的判定,空间图形的公理,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)要证四点共线,只需找到一个平面,是这四个点在这个平面内,用确定平面的方法,两条平行线确定一个平面,即可证出;
(2)要证明两个平面垂直,只需证明其中一个平面经过另一个平面的一条垂线即可,也就是只需证线面垂直即可,而要证线面垂直,只需证明这条直线垂直平面内的两条相交直线,这样,一步步寻找成立的条件.
(3)求异面直线所成角,先平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成角就是异面直线所成角或其补角,再放入三角形中计算即可.
(2)要证明两个平面垂直,只需证明其中一个平面经过另一个平面的一条垂线即可,也就是只需证线面垂直即可,而要证线面垂直,只需证明这条直线垂直平面内的两条相交直线,这样,一步步寻找成立的条件.
(3)求异面直线所成角,先平移两条异面直线中的一条,使它们成为相交直线,则相交直线所成角就是异面直线所成角或其补角,再放入三角形中计算即可.
解答:
 (1)证明:由条件有PQ为△ADE的中位线,MN为梯形BCDE的中位线,
(1)证明:由条件有PQ为△ADE的中位线,MN为梯形BCDE的中位线,
∴PQ∥DE,MN∥DE,
∴PQ∥MN
∴M、N、P、Q四点共面.…(3分)
(2)证明:由等腰直角三角形ABC有AD⊥DE,CD⊥DE,DE∥BC
又AD∩CD=D,
∴DE⊥面ACD,
又DE∥BC
∴BC⊥平面ACD,
∵BC?平面ABC,
∴平面ABC⊥平面ACD…(6分)
(3)解:由条件知AD=1,DC=1,BC=2,
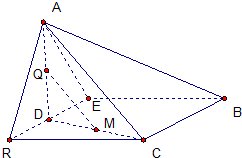
延长ED到R,使DR=ED,连结RC …(8分)
则ER=BC,ER∥BC,故BCRE为平行四边形 …(10分)
∴RC∥EB,又AC∥QM
∴∠ACR为异面直线BE与QM所成的角θ(或θ的补角)…(11分)
∵DA=DC=DR,且三线两两互相垂直,
∴由勾股定理得AC=AR=RC=
,…(12分)
∵△ACR为正三角形,
∴∠ACR=60°,
∴异面直线BE与QM所成的角大小为60°.…(13分)
 (1)证明:由条件有PQ为△ADE的中位线,MN为梯形BCDE的中位线,
(1)证明:由条件有PQ为△ADE的中位线,MN为梯形BCDE的中位线,∴PQ∥DE,MN∥DE,
∴PQ∥MN
∴M、N、P、Q四点共面.…(3分)
(2)证明:由等腰直角三角形ABC有AD⊥DE,CD⊥DE,DE∥BC
又AD∩CD=D,
∴DE⊥面ACD,
又DE∥BC
∴BC⊥平面ACD,
∵BC?平面ABC,
∴平面ABC⊥平面ACD…(6分)
(3)解:由条件知AD=1,DC=1,BC=2,
延长ED到R,使DR=ED,连结RC …(8分)
则ER=BC,ER∥BC,故BCRE为平行四边形 …(10分)
∴RC∥EB,又AC∥QM
∴∠ACR为异面直线BE与QM所成的角θ(或θ的补角)…(11分)
∵DA=DC=DR,且三线两两互相垂直,
∴由勾股定理得AC=AR=RC=
| 2 |
∵△ACR为正三角形,
∴∠ACR=60°,
∴异面直线BE与QM所成的角大小为60°.…(13分)
点评:本题考查了平面垂直,四点共线,以及异面直线所成角的求法,是立体几何中的常规题,应当掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
由直线y=0,x=e,y=2x及曲线y=
所围成的封闭的图形的面积为( )
| 2 |
| x |
| A、3 |
| B、3+2ln2 |
| C、e2-3 |
| D、e |
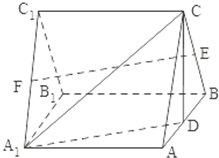 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.