题目内容
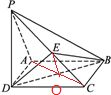
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E为PC的中点.(1)证明:PA∥平面BDE;
(2)证明:平面PAC⊥平面PDB.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连接AC交BD于点O,连接EO,求证出EO是△PAC的中位线,得出EO∥PA,继而PA∥平面BDE;
(2)要证明平面PAC⊥平面PDB,只要证明AC⊥平面PBD,而根据已知条件可以求出.
(2)要证明平面PAC⊥平面PDB,只要证明AC⊥平面PBD,而根据已知条件可以求出.
解答:
解:(1)连接AC交BD于点O,连接EO,
∵ABCD是正方形,
∴A0=CO,
∵E为PC的中点,
∴EO是△PAC的中位线,
∴EO∥PA,
又EO?平面BDE,
∴PA∥平面BDE
(2)∵PD⊥平面ABCD,AC?平面ABCD
∴PD⊥AC,
∵ABCD是正方形,
∴BD⊥AC,
又PD∩BD=D,
∴AC⊥平面PBD,
又AC?平面PAC,
∴平面PAC⊥平面PDB.
 ,
,
∵ABCD是正方形,
∴A0=CO,
∵E为PC的中点,
∴EO是△PAC的中位线,
∴EO∥PA,
又EO?平面BDE,
∴PA∥平面BDE
(2)∵PD⊥平面ABCD,AC?平面ABCD
∴PD⊥AC,
∵ABCD是正方形,
∴BD⊥AC,
又PD∩BD=D,
∴AC⊥平面PBD,
又AC?平面PAC,
∴平面PAC⊥平面PDB.
 ,
,
点评:本题考查了线面平行的判定定理,以及面面垂直的判定定理,关键是转化为线线的位置关系.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
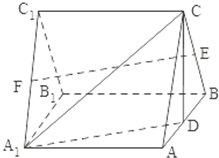 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.