题目内容
已知f(x)=loga
(a>0,a≠1).
(Ⅰ)求f(x)的定义域;
(Ⅱ)判断f(x)的奇偶性并予以证明;
(Ⅲ)写出f(x)的单调区间.(不必证明)
| 1+x |
| 1-x |
(Ⅰ)求f(x)的定义域;
(Ⅱ)判断f(x)的奇偶性并予以证明;
(Ⅲ)写出f(x)的单调区间.(不必证明)
考点:奇偶性与单调性的综合,函数的定义域及其求法
专题:函数的性质及应用
分析:(I)根据对数函数的真数部分必为正,构造不等式,可求出函数的定义域;
(II)由已知中函数解析式,求出f(-x)的解析式,并根据对数的运算性质,判断出f(-x)与f(x)的关系,进而根据函数奇偶性的定义,判断出函数为奇函数;
(III)根据对数函数单调性与底数的关系及复合函数同增异减的原则,可得到函数的单调区间.
(II)由已知中函数解析式,求出f(-x)的解析式,并根据对数的运算性质,判断出f(-x)与f(x)的关系,进而根据函数奇偶性的定义,判断出函数为奇函数;
(III)根据对数函数单调性与底数的关系及复合函数同增异减的原则,可得到函数的单调区间.
解答:
解:(Ⅰ)由对数函数的定义知
>0
解得-1<x<1
故f (x)的定义域为(-1,1)…(4分)
(Ⅱ)∵f(x)=loga
∴f(-x)=loga
=-loga
=-f(x),
∴f (x)为奇函数…(8分)
(Ⅲ)故当a>1时,f(x)在区间(-1,1)单调递增;
当0<a<1时,f(x)在区间(-1,1)单调递减.…(12分)
| 1+x |
| 1-x |
解得-1<x<1
故f (x)的定义域为(-1,1)…(4分)
(Ⅱ)∵f(x)=loga
| 1+x |
| 1-x |
∴f(-x)=loga
| 1-x |
| 1+x |
| 1+x |
| 1-x |
∴f (x)为奇函数…(8分)
(Ⅲ)故当a>1时,f(x)在区间(-1,1)单调递增;
当0<a<1时,f(x)在区间(-1,1)单调递减.…(12分)
点评:本题考查的知识点是函数的定义域,函数的奇偶性,函数的单调性,熟练掌握对数函数的图象和性质是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
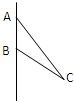 如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是
如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是