题目内容
已知函数f(x)与g(x)满足f(2+x)=f(2-x),g(x+1)=g(x-1),且f(x)在区间[2,+∞)上为减函数,令h(x)=f(x)•|g(x)|,则下列不等式正确的有 .
①h(-2)≥h(4)
②h(-2)≤h(4)
③h(0)>h(4)
④h(0)=h(4).
①h(-2)≥h(4)
②h(-2)≤h(4)
③h(0)>h(4)
④h(0)=h(4).
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由已知中函数f(x)与g(x)满足f(2+x)=f(2-x),g(x+1)=g(x-1),且f(x)在区间[2,+∞)上为减函数,可判断出f(4)=f(0),f(-2)<f(4),及g(-2)=g(0)=g(2)=g(4),结合不等式的基本性质可得答案.
解答:
解:∵函数f(x)满足f(2+x)=f(2-x),
故函数f(x)的图象关于直线x=2对称
当x=2时,f(4)=f(0)…①
又∵f(x)在区间[2,+∞)上为减函数,
∴f(x)在区间(-∞,2]上为增函数,
当x=4时,f(6)=f(-2)<f(4)…②
又∵g(x+1)=g(x-1),故函数g(x)是又2为周期的周期函数
g(-2)=g(0)=g(2)=g(4)…③,
∵h(x)=f(x)•|g(x)|,
由①③得:h(0)=h(4).
由①②得:h(-2)≤h(4)
故答案为:②④
故函数f(x)的图象关于直线x=2对称
当x=2时,f(4)=f(0)…①
又∵f(x)在区间[2,+∞)上为减函数,
∴f(x)在区间(-∞,2]上为增函数,
当x=4时,f(6)=f(-2)<f(4)…②
又∵g(x+1)=g(x-1),故函数g(x)是又2为周期的周期函数
g(-2)=g(0)=g(2)=g(4)…③,
∵h(x)=f(x)•|g(x)|,
由①③得:h(0)=h(4).
由①②得:h(-2)≤h(4)
故答案为:②④
点评:本题考查的知识点是抽象函数及其应用,函数的对称性,函数的周期性,不等式的基本性质,其中根据已知分析出f(4)=f(0),f(-2)<f(4),及g(-2)=g(0)=g(2)=g(4)是解答的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的表面积为( )
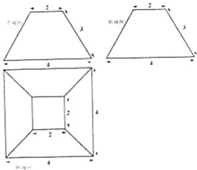

A、20+12
| ||
B、20+24
| ||
C、20+12
| ||
| D、56 |
若对任意的x∈R,函数f(x)满足f(x+1)=-f(x),且f(2013)=-2013,则f(-1)=( )
| A、1 | B、-1 |
| C、2013 | D、-2013 |