题目内容
(1)求证:3(1+a2+a4)≥(1+a+a2)2
(2)已知:a2+b2=1,m2+n2=2,证明:-
≤am+bn≤
.
(2)已知:a2+b2=1,m2+n2=2,证明:-
| 2 |
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:(1)运用作差法,由三个数和的平方公式,运用因式分解方法,即可得证;
(2)运用三角换元,可令a=cosα,b=sinα,m=
cosβ,n=
sinβ,α,β∈R,运用两角和的余弦公式和余弦函数的值域,即可得证.
(2)运用三角换元,可令a=cosα,b=sinα,m=
| 2 |
| 2 |
解答:
证明:(1)∵3(1+a2+a4)-(1+a+a2)2
=3+3a2+3a4-(1+a2+a4+2a+2a3+2a2)
=2a4+2-2a-2a3
=2(a4-a3)+2(1-a)
=2(a-1)(a3-1)
=2(a-1)2(a2+a+1)=2(a-1)2[(a+
)2+
]≥0,
∴3(1+a2+a4)≥(1+a+a2)2
(2)∵a2+b2=1,m2+n2=2,
∴可令a=cosα,b=sinα,m=
cosβ,n=
sinβ,α,β∈R,
∴am+bn=
cosαcosβ+
sinαsinβ
=
(cosαcosβ+sinαsinβ)=
cos(α-β),
∵-1≤cos(α-β)≤1,
∴-
≤am+bn≤
.
=3+3a2+3a4-(1+a2+a4+2a+2a3+2a2)
=2a4+2-2a-2a3
=2(a4-a3)+2(1-a)
=2(a-1)(a3-1)
=2(a-1)2(a2+a+1)=2(a-1)2[(a+
| 1 |
| 2 |
| 3 |
| 4 |
∴3(1+a2+a4)≥(1+a+a2)2
(2)∵a2+b2=1,m2+n2=2,
∴可令a=cosα,b=sinα,m=
| 2 |
| 2 |
∴am+bn=
| 2 |
| 2 |
=
| 2 |
| 2 |
∵-1≤cos(α-β)≤1,
∴-
| 2 |
| 2 |
点评:本题考查不等式的证明方法:作差法和换元法,考查推理能力,属于中档题.

练习册系列答案
相关题目
“B=60°”是“△ABC三个内角成等差数列”的( )
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、既不充分又非必要条件. |
若|
|=|
|=|
•
|,则
与
+
的夹角为( )
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、150° | D、120° |
函数y=sinα+cosα的图象的一个对称中心是( )
A、(
| ||||
B、(
| ||||
C、(-
| ||||
D、(
|
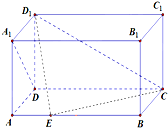 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=