题目内容
某公司生产某种产品投入固定资本20万元,以后生产x万件产品需要再投入可变资本a(x2-1)万元,收入资金为R(x)=160x-3.8x2-1480.2万元,已知当生产10万件产品时,投入生产资金可达到39.8万元.
(1)判断生产每件产品所需可变资本函数的单调性;
(2)求计划生产多少件产品时,利润最大?最大是多少?
(1)判断生产每件产品所需可变资本函数的单调性;
(2)求计划生产多少件产品时,利润最大?最大是多少?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)利用当生产10万件产品时,投入生产资金可达到39.8万元,求出a,可得函数解析式,利用导数,可得生产每件产品所需可变资本函数的单调性;
(2)确定函数解析式,利用配方法求最值即可.
(2)确定函数解析式,利用配方法求最值即可.
解答:
解:(1)由题意得:
=39.8-20,解得a=2,
∴生产每件产品所需可变资本函数y=2x-
,
∵y′=2+
,∴生产每件产品所需可变资本函数为增函数;
(2)设计划生产x件产品时利润f(x)最大,则有f(x)=160x-3.8x2-1480.2-2(x2-1)=-5.8x2+160x-1478.2,
故当x=
万件时,利润最大.最大利润为f(
)=705.9万元.
| a(100-1) |
| 10 |
∴生产每件产品所需可变资本函数y=2x-
| 2 |
| x |
∵y′=2+
| 2 |
| x2 |
(2)设计划生产x件产品时利润f(x)最大,则有f(x)=160x-3.8x2-1480.2-2(x2-1)=-5.8x2+160x-1478.2,
故当x=
| 400 |
| 29 |
| 400 |
| 29 |
点评:本题考查函数模型的选择与应用,考查导数知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知点A(-1,1,0)、B(1,2,0)、C(-2,-1,0)、D(3,4,0),则
在
方向的投影为( )
| AB |
| CD |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
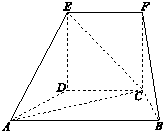 如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.
如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,且平面CDEF⊥平面ABCD.