题目内容
8.(1)已知tan(π+α)=-$\frac{1}{3}$,求$\frac{sinα+2cosα}{5cosα-sinα}$的值;(Ⅱ)已知sinα-cosα=$\frac{1}{5}$,且0<α<π,求tanα的值.
分析 由条件利用本题主要考查同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)∵已知tan(π+α)=-$\frac{1}{3}$,∴$\frac{sinα+2cosα}{5cosα-sinα}$=$\frac{tanα+2}{5-tanα}$=$\frac{\frac{5}{3}}{\frac{16}{3}}$=$\frac{5}{16}$.
(Ⅱ)∵已知sinα-cosα=$\frac{1}{5}$,∴1-2sinαcosα=$\frac{1}{25}$,∴2sinαcosα=$\frac{24}{25}$,
∵0<α<π,∴sinα>0、cosα>0,∴sinα+cosα=$\sqrt{{(sinα+cosα)}^{2}}$=$\sqrt{1+\frac{24}{25}}$=$\frac{7}{5}$,
∴sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$,∴tanα=$\frac{sinα}{cosα}$=$\frac{4}{3}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
19.函数f(x)的图象如图所示,则下列结论正确的是( )
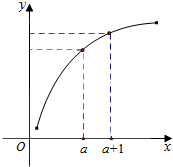

| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
16.已知集合A={x|0<x<3},B=$\left\{{x|y=\sqrt{{x^2}-1}}\right\}$,则集合A∩(∁RB)为( )
| A. | [0,1) | B. | (0,1) | C. | [1,3) | D. | (1,3) |
3.若角α的顶点为坐标原点,始边与x轴的非负半轴重合,且终边上一点的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则tanα的值为( )
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
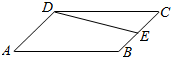

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
18.若m>n,则( )
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |
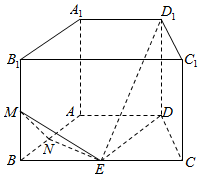 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.