题目内容
13.在△ABC中,角A,B,C的对边分别为a,b,c,且($\sqrt{3}$c-2b)cos(π-A)=$\sqrt{3}$acosC,(1)求角A的值;
(2)若角B=$\frac{π}{6}$,BC边上的中线AM的长为$\sqrt{7}$,求△ABC的面积.
分析 (1)利用正弦定理将边化角,使用和角公式化简即可得出cosA;
(2)使用余弦定理解出等腰三角形的腰长,代入面积公式计算.
解答 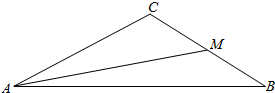 解:(1)在△ABC中,∵($\sqrt{3}$c-2b)cos(π-A)=$\sqrt{3}$acosC,
解:(1)在△ABC中,∵($\sqrt{3}$c-2b)cos(π-A)=$\sqrt{3}$acosC,
∴(2sinB-$\sqrt{3}$sinC)cosA=$\sqrt{3}$sinAcosC,
即2sinBcosA=$\sqrt{3}$sinAcosC+$\sqrt{3}$sinCcosA=$\sqrt{3}$sin(A+C)=$\sqrt{3}$sinB.
∴cosA=$\frac{\sqrt{3}}{2}$.∴A=$\frac{π}{6}$.
(2)∵A=B=$\frac{π}{6}$,∴AC=BC,C=$\frac{2π}{3}$.设CM=x,则AC=2x,
在△ACM中,由余弦定理得AM2=AC2+CM2-2AC•CMcosC,
即7=4x2+x2+2x2,解得x=1,∴AC=BC=2.
∴S△ABC=$\frac{1}{2}AC•BCsinC$=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
3.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线经过点(3,$\sqrt{3}$),则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\frac{2\sqrt{3}}{3}$或2 | D. | $\sqrt{3}$或2 |
7.已知定义在R上的奇函数f (x)满足f(x)=f(4-x),且在区间[0,2]上是增函数,那么( )
| A. | f(6)<f(4)<f(1) | B. | f(4)<f(6)<f(1) | C. | f(1)<f(6)<f(4) | D. | f(6)<f(1)<f(4) |