题目内容
3.若角α的顶点为坐标原点,始边与x轴的非负半轴重合,且终边上一点的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则tanα的值为( )| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
分析 利用三角函数的定义,即可得出结论.
解答 解:∵点(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)是角α终边上一点,
∴tanα=-$\sqrt{3}$,
故选:A.
点评 本题考查三角函数的定义,考查学生的计算能力,比较基础.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18.已知α∈(0,$\frac{π}{2}$),且cos(α+$\frac{π}{3}$)=-$\frac{3}{5}$,则sinα的值为( )
| A. | $\frac{3-4\sqrt{3}}{10}$ | B. | $\frac{3+4\sqrt{3}}{10}$ | C. | $\frac{4-3\sqrt{3}}{10}$ | D. | $\frac{4+3\sqrt{3}}{10}$ |
12.下列函数中,既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=lnx | B. | y=x3 | C. | y=x2 | D. | y=sinx |
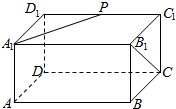 如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.
如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.