题目内容

19．函数f（x）的图象如图所示，则下列结论正确的是（　　）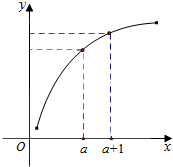
A．0＜f′（a）＜f′（a+1）＜f（a+1）-f（a）B．0＜f′（a+1）＜f（a+1）-f（a）＜f′（a）
C．0＜f′（a+1）＜f′（a）＜f（a+1）-f（a）D．0＜f（a+1）-f（a）＜f′（a）＜f′（a+1）

分析 根据函数的变化率和导数的几何意义进行判断．

解答 解：f（a+1）-f（a）=$\frac{f（a+1）-f（a）}{（a+1）-a}$=f′（x0），x0∈（a，a+1）．
∵函数是增函数，且增长速度逐渐变慢，∴函数切线的斜率逐渐变小，
∴0＜f′（a+1）＜f（a+1）-f（a）＜f′（a）．
故选：B．

点评 本题考查了导数的几何意义，变化率的概念，属于基础题．

练习册系列答案
相关题目
4．已知cosα=$\frac{1}{2}$，且α是第四象限的角，求sinα和tanα．
10．已知数列{an}中，a1=2，a2=3，an＞0，且满足an+12-an=an+1+an2（n∈N*）．
（1）求数列{an}的通项公式；
（2）设${b_n}={2^n}•{a_n}$，求数列{bn}的前n项和Tn；
（3）设${C_n}={4^n}-λ•{2^{a_n}}$（λ为正偶数，n∈N*），是否存在确定λ的值，使得对任意n∈N*，有Cn+1＞Cn恒成立，若存在，求出λ的值，若不存在，说明理由．
7．已知定义在R上的奇函数f （x）满足f（x）=f（4-x），且在区间[0，2]上是增函数，那么（　　）
A．f（6）＜f（4）＜f（1）B．f（4）＜f（6）＜f（1）C．f（1）＜f（6）＜f（4）D．f（6）＜f（1）＜f（4）
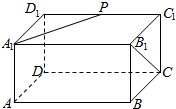14．如图，在长方体ABCD-A1B1C1D1中，设 AD=AA1=1，AB=2，P是C1D1的中点，则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°，$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1．
4．定义在（0，+∞）上的函数f（x），如果对任意x∈（0，+∞），都有f（kx）=kf（x）（k≥2，k∈N*）成立，则称f（x）为k阶伸缩函数．
（Ⅰ）若函数f（x）为二阶伸缩函数，且当x∈（1，2]时，$f（x）=1+{log_{\frac{1}{3}}}x$，求$f（2\sqrt{3}）$的值；
（Ⅱ）若函数f（x）为三阶伸缩函数，且当x∈（1，3]时，$f（x）=\sqrt{3x-{x^2}}$，求证：函数$y=f（x）-\sqrt{2}x$在（1，+∞）上无零点；
（Ⅲ）若函数f（x）为k阶伸缩函数，且当x∈（1，k]时，f（x）的取值范围是[0，1），求f（x）在（0，kn+1]（n∈N*）上的取值范围．
11．已知圆C经过A（1，3），B（-1，1）两点，且圆心在直线y=x上．
（Ⅰ）求圆C的方程；
（Ⅱ）设直线l经过点（2，-2），且l与圆C相交所得弦长为$2\sqrt{3}$，求直线l的方程．
8．（1）已知tan（π+α）=-$\frac{1}{3}$，求$\frac{sinα+2cosα}{5cosα-sinα}$的值；
（Ⅱ）已知sinα-cosα=$\frac{1}{5}$，且0＜α＜π，求tanα的值．
9．在等差数列{an}中，已知a1=2，S9=54，若数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为$\frac{7}{16}$，则n=14．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网