题目内容
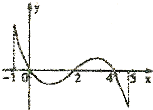 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 2 | 4 | 5 |
| F(x) | 1 | 2 | 1.5 | 2 | 1 |
②函数f(x)在[0,2]上是减函数;
③当1<a<2时,函数y=f(x)-a最多有4个零点;
④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4.
考点:导数的运算,函数单调性的判断与证明,根的存在性及根的个数判断
专题:导数的综合应用
分析:由导函数的图象看出函数的单调区间及原函数的极值点,结合函数f(x)在定义域[-1,5]内的部分对应值表,可以作出函数f(x)图象的大致形状,由图象形状可以判断四个命题的真假.
解答:
解:由导函数的图象可知:
根据上述表格及其已知表格可画出函数f(x)的图象:
①由原图标可知,函数f(x)的值域为[1,2],①正确;
②函数y=f(x)在[0,2]上的导数小于等于0,函数f(x)在[0,2]是减函数,②正确;
③作出函数y=a的图象,
可知:当1<a<2时,函数y=f(x)与y=a有四个交点,
因此函数y=f(x)-a有4个零点,③正确;
④∵函数f(x)在[-1,5]上的最大值为2,故如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,④不正确.
综上可知:①②③正确.
故答案为:①②③.
| x | [-1,0) | 0 | (0,2) | 2 | (2,4) | 4 | (4,5] |
| f′(x) | + | 0 | - | 0 | + | 0 | - |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
①由原图标可知,函数f(x)的值域为[1,2],①正确;

②函数y=f(x)在[0,2]上的导数小于等于0,函数f(x)在[0,2]是减函数,②正确;
③作出函数y=a的图象,
可知:当1<a<2时,函数y=f(x)与y=a有四个交点,
因此函数y=f(x)-a有4个零点,③正确;
④∵函数f(x)在[-1,5]上的最大值为2,故如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,④不正确.
综上可知:①②③正确.
故答案为:①②③.
点评:题考查的是判断命题的真假,考查了利用导数研究函数的极值,考查了数形结合的解题思想,解答此题的关键是通过导函数的图象得到原函数的单调区间及极值点的情况,属中档题.

练习册系列答案
相关题目
已知函数f(x)=lg(|x|+1),定义函数F(x)=
,若mn<0,m+n>0,则有F(m)+F(n)( )
|
| A、一定为负数 | B、等于0 |
| C、一定为正数 | D、正负不能确定 |
函数f(x)=
,若f(-a)+f(a)≤2f(1),则实数a取值范围是( )
|
| A、(-∞,-1]∪[1,+∞) |
| B、[-1,0] |
| C、[0,1] |
| D、[-1,1] |
在△ABC中,已知b=3,c=3
,A=30°,则角C等于( )
| 3 |
| A、30° | B、60°或120° |
| C、60° | D、120° |
已知函数f(x)=
,则f(2014)=( )
|
| A、2012 | B、2013 |
| C、2014 | D、2015 |
在等差数列{an}中,Sn为数列{an}的前n项和,若3a3=a13,则
等于( )
| S10 |
| S5 |
| A、1 | B、2 | C、3 | D、4 |