题目内容
已知函数f(x)=
,则f(2014)=( )
|
| A、2012 | B、2013 |
| C、2014 | D、2015 |
考点:抽象函数及其应用,函数的值
专题:函数的性质及应用
分析:利用赋值法,先令x=1,求出f(1),再令x=2,求出f(2),令x=n,则f(n)-f(n-1)=1,再根据等差数列的通项求出f(2014).
解答:
解:当x=1时,f(1)=log5(5-1)=2,
当x>1时,f(x)=f(x-1)+1,
令x=2,则f(2)=f(1)+1=2+1=3,
令x=n,则f(n)-f(n-1)=1,
∴{f(n)}是以2为首项,以1为公差的等差数列,
∴f(2014)=2+(2014-1)×1=2015,
故选:D
当x>1时,f(x)=f(x-1)+1,
令x=2,则f(2)=f(1)+1=2+1=3,
令x=n,则f(n)-f(n-1)=1,
∴{f(n)}是以2为首项,以1为公差的等差数列,
∴f(2014)=2+(2014-1)×1=2015,
故选:D
点评:本题主要考查了抽象函数的问题,关键转化为{f(n)}是以2为首项,以1为公差的等差数列,属于基础题.

练习册系列答案
相关题目
由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为( )
A、
| ||
| B、2-ln 3 | ||
| C、4+ln 3 | ||
| D、4-ln 3 |
在△ABC中,若a2sinC=bcsinA,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
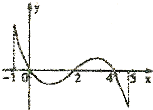 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题: