题目内容
袋中有5个大小相同的小球,其中1个白球和4个黑球,每次从中任取一球,每次取出的黑球不再放回去,直到取出白球为止.求取球次数X的期望和方差.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:由题意知X的所有可能取值为:1,2,3,4,5,由此能求出取球次数X的期望和方差.
解答:
解:由题意知X的所有可能取值为:1,2,3,4,5,
P(X=1)=
,
P(X=2)=
×
=
,
P(X=3)=
×
×
=
,
P(X=4)=
×
×
×
=
,
P(X=5)=
×
×
×
×1=
,
∴E(X)=(1+2+3+4+5)×
=3,
D(X)=(1-3)2×
+…+(5-3)2×
=2.
P(X=1)=
| 1 |
| 5 |
P(X=2)=
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
P(X=3)=
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
P(X=4)=
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
P(X=5)=
| 4 |
| 5 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
∴E(X)=(1+2+3+4+5)×
| 1 |
| 5 |
D(X)=(1-3)2×
| 1 |
| 5 |
| 1 |
| 5 |
点评:本题考查离散型随机变量的数学期望和方差的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
在△ABC中,已知三边a=3,b=5,c=7,则三角形ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
已知f(x)=
,则f(3)=( )
|
A、
| ||
B、-
| ||
| C、-1 | ||
| D、3 |
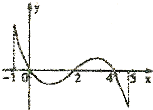 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题: