题目内容
数列{an}的通项公式为an=2n-29,Sn达到最小时,n等于 .
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:由已知可判断数列为等差数列,并且可得等差数列{an}的前14项为负值,从第55项开始为正值,由出现正项前的和最小可得答案.
解答:
解:由an=2n-29可得
an+1-an=2(n+1)-29-(2n-29)=2为常数,
∴可得数列{an}为等差数列,
令2n-49≥0可得,n≥
,
故等差数列{an}的前14项为负值,从第15项开始为正值,
故前14项和最小.
故答案为14.
an+1-an=2(n+1)-29-(2n-29)=2为常数,
∴可得数列{an}为等差数列,
令2n-49≥0可得,n≥
| 29 |
| 2 |
故等差数列{an}的前14项为负值,从第15项开始为正值,
故前14项和最小.
故答案为14.
点评:本题考查等差数列的性质,由数列自身的变化得到答案是解决问题的捷径,属基础题.

练习册系列答案
相关题目
已知S(t)是由函数f(x)=
-
的图象,g(x)=|x-2|-2的图象与直线x=t围成的图形的面积,则函数S(t)的导函数y=S′(t)(0<t<4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
A、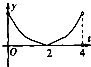 |
B、 |
C、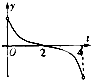 |
D、 |
在△ABC中,若a2sinC=bcsinA,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
将函数y=cos(
x-
)的图象上各点向左平移
个单位,所得函数图象的一条对称轴是( )
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
D、x=
|
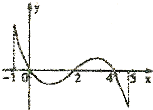 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题: