题目内容
已知命题p:
≤-1,命题q:x2-x<a2-a,且?q的一个充分不必要条件是?p,则实数a的取值范围是 .
| 4 |
| x-1 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:命题p:
≤-1,转化为一元二次不等式,解得-3≤x<1.由于?q的一个充分不必要条件是?p,
可得p是q充分不必要条件,及命题q:x2-x<a2-a,可得a2-a>(x2-x)max,x∈[-3,1).再利用二次函数的单调性即可解出.
| 4 |
| x-1 |
可得p是q充分不必要条件,及命题q:x2-x<a2-a,可得a2-a>(x2-x)max,x∈[-3,1).再利用二次函数的单调性即可解出.
解答:
解:命题p:
≤-1,化为
≤0,即(x-1)(x+3)≤0,且x-1≠0,解得-3≤x<1;
∵?q的一个充分不必要条件是?p,
∴p是q充分不必要条件.
∵命题q:x2-x<a2-a,
∴a2-a>(x2-x)max,x∈[-3,1).
令f(x)=x2-x=(x-
)2+
≤f(-3)=12,
∴a2-a>12,
解得a>4或a<-3.
∴实数a的取值范围是(-∞,-3)∪(4,+∞).
故答案为:(-∞,-3)∪(4,+∞).
| 4 |
| x-1 |
| x+3 |
| x-1 |
∵?q的一个充分不必要条件是?p,
∴p是q充分不必要条件.
∵命题q:x2-x<a2-a,
∴a2-a>(x2-x)max,x∈[-3,1).
令f(x)=x2-x=(x-
| 1 |
| 2 |
| 3 |
| 4 |
∴a2-a>12,
解得a>4或a<-3.
∴实数a的取值范围是(-∞,-3)∪(4,+∞).
故答案为:(-∞,-3)∪(4,+∞).
点评:本题考查了一元二次不等式的解法、二次函数的单调性、简易逻辑的判定,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列函数中,在区间(1,+∞)上是增函数的是( )
| A、y=-x+1 | ||
B、y=-
| ||
| C、y=x2-4x+3 | ||
D、y=
|
某工厂某种产品的产量y(千件)与单位成本x(元)之间的关系满足y=60-2.5x,则以下说法正确的是( )
| A、产品每增加1 000 件,单位成本下降2.5万元 |
| B、产品每减少1 000 件,单位成本上升2.5万元 |
| C、产品每增加1 000 件,单位成本上升2.5万元 |
| D、产品每减少1 000 件,单位成本下降2.5万元 |
已知a>b>c,a+b+c=0,当0<x<1时,代数式ax2+bx+c的值是( )
| A、正数 | B、负数 |
| C、0 | D、介于-1与0之间 |
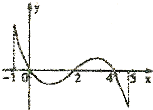 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题: