题目内容
在△ABC中,已知b=3,c=3
,A=30°,则角C等于( )
| 3 |
| A、30° | B、60°或120° |
| C、60° | D、120° |
考点:正弦定理
专题:解三角形
分析:由条件利用余弦定理求得a=3=b,可得A=B=30°,从而求得C的值.
解答:
解:△ABC中,∵已知b=3,c=3
,A=30°,则由余弦定理可得a2=b2+c2-2bc•cosA=9+27-18
•
=9,故a=3,
故有a=b,∴A=B=30°,∴C=120°,
故选:D.
| 3 |
| 3 |
| ||
| 2 |
故有a=b,∴A=B=30°,∴C=120°,
故选:D.
点评:本题主要考查余弦定理的应用,根据三角函数的值求角,属于基础题.

练习册系列答案
相关题目
在△ABC中,已知三边a=3,b=5,c=7,则三角形ABC是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
已知S(t)是由函数f(x)=
-
的图象,g(x)=|x-2|-2的图象与直线x=t围成的图形的面积,则函数S(t)的导函数y=S′(t)(0<t<4)的大致图象是( )
| 1 |
| |x-2|+1 |
| 1 |
| 3 |
A、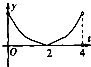 |
B、 |
C、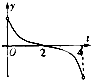 |
D、 |
将函数y=cos(
x-
)的图象上各点向左平移
个单位,所得函数图象的一条对称轴是( )
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
A、x=
| ||
B、x=
| ||
| C、x=π | ||
D、x=
|
某工厂某种产品的产量y(千件)与单位成本x(元)之间的关系满足y=60-2.5x,则以下说法正确的是( )
| A、产品每增加1 000 件,单位成本下降2.5万元 |
| B、产品每减少1 000 件,单位成本上升2.5万元 |
| C、产品每增加1 000 件,单位成本上升2.5万元 |
| D、产品每减少1 000 件,单位成本下降2.5万元 |
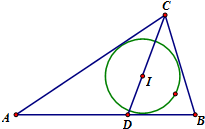 如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若
如图,△ABC中,点A(-1,0),B(1,0).圆I是△ABC的内切圆,且CI延长线交AB与点D,若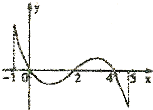 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题: