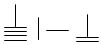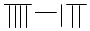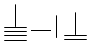题目内容
15.已知椭圆Γ:$\frac{x^2}{a^2}$+y2=1(a>1)的左焦点为F1,右顶点为A1,上顶点为B1,过F1,A1,B1三点的圆P的圆心坐标为($\frac{{\sqrt{3}-\sqrt{2}}}{2}$,$\frac{{1-\sqrt{6}}}{2}$).(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l:y=kx+m(k,m为常数,k≠0)与椭圆Γ交于不同的两点M和N.
(i)当直线l过E(1,0),且$\overrightarrow{EM}$+2$\overrightarrow{EN}$=$\overrightarrow 0$时,求直线l的方程;
(ii)当坐标原点O到直线l的距离为$\frac{{\sqrt{3}}}{2}$时,且△MON面积为$\frac{{\sqrt{3}}}{2}$时,求直线l的倾斜角.
分析 (Ⅰ)由题可知:圆心P在A1F1的中垂线上,则a-c=$\sqrt{3}$-$\sqrt{2}$,由椭圆的性质可知:a2-c2=1,即可求得a的值,求得椭圆方程;
(Ⅱ)(i)设直线l的方程为y=k(x-1),代入椭圆方程,利用韦达定理及向量的坐标运算,即可求得x1及x2,由x1x2=$\frac{3{k}^{2}-3}{1+3{k}^{2}}$,代入即可求得k的值,求得直线l的方程;
(ii)将直线l的方程代入椭圆方程,由点到直线的距离公式求得m2=$\frac{3}{4}$(k2+1),利用韦达定理,弦长公式,三角形的面积公式即可求得三角形面积表达式,由△MON面积为$\frac{{\sqrt{3}}}{2}$,即可求得k的值,求得直线l的倾斜角.
解答 解:(Ⅰ)椭圆Γ:$\frac{x^2}{a^2}$+y2=1(a>1)的左焦点为F1(-c,0)右顶点为A1(a,0)上顶点为B1(0,1),
由题意可知,圆心P在A1F1的中垂线上,即$\frac{a-c}{2}$=$\frac{{\sqrt{3}-\sqrt{2}}}{2}$,则a-c=$\sqrt{3}$-$\sqrt{2}$,
由a2-c2=1,及(a+c)(a-c)=1,∴a+c=$\sqrt{3}$+$\sqrt{2}$,
∴a=$\sqrt{3}$,c=$\sqrt{2}$,
∴椭圆的标准方程为:$\frac{{x}^{2}}{3}+{y}^{2}=1$;
(Ⅱ)(i)设直线l的方程为y=k(x-1),M(x1,y1),N(x2,y2),.
代入椭圆方程,整理得:(1+3k2)x2-6k2x+3k2-3=0,
由韦达定理可知:x1+x2=$\frac{6{k}^{2}}{1+3{k}^{2}}$,①x1x2=$\frac{3{k}^{2}-3}{1+3{k}^{2}}$,②
由$\overrightarrow{EM}$=(x1-1,y1),$\overrightarrow{EN}$=(x2-1,y2)$\overrightarrow 0$,
$\overrightarrow{EM}$+2$\overrightarrow{EN}$=$\overrightarrow 0$时,则(x1-1,y1)+2(x2-1,y2)=$\overrightarrow{0}$,则x1+2x2=3,③,
由①③,解得:x1=$\frac{3{k}^{2}-3}{1+3{k}^{2}}$,x2=$\frac{3+3{k}^{2}}{1+3{k}^{2}}$
由②可知:$\frac{3{k}^{2}-3}{1+3{k}^{2}}$=$\frac{3{k}^{2}-3}{1+3{k}^{2}}$×$\frac{3+3{k}^{2}}{1+3{k}^{2}}$,
当3k2-3=0时,即k=±1,显然成立,
当3k2-3≠0,1+3k2≠0,则$\frac{3+3{k}^{2}}{1+3{k}^{2}}$=1,显然不成立,
综上可知:k=±1,
∴直线l的方程y=x-1或y=-x+1;
(ii)设M(x1,y1),N(x2,y2).
由题意,设直线AB的方程为y=kx+m,
由坐标原点O到直线l的距离为$\frac{\sqrt{3}}{2}$可得$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$,化为m2=$\frac{3}{4}$(k2+1).
把y=kx+m代入椭圆方程,消去y得到(3k2+1)x2+6kmx+3m2-3=0,
∴x1+x2=-$\frac{6km}{3{k}^{2}+1}$,x1x2=$\frac{3{m}^{2}-3}{3{k}^{2}+1}$.
∴丨MN丨2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)[(-$\frac{6km}{3{k}^{2}+1}$)2-4($\frac{3{m}^{2}-3}{3{k}^{2}+1}$)]=$\frac{12({k}^{2}+1)(3{k}^{2}+1-{m}^{2})}{(3{k}^{2}+1)^{2}}$=$\frac{3({k}^{2}+1)(9{k}^{2}+1)}{(3{k}^{2}+1)^{2}}$,
由△MON面积S2=($\frac{1}{2}$×丨MN丨×$\frac{\sqrt{3}}{2}$)2,
=$\frac{3}{16}$×$\frac{3({k}^{2}+1)(9{k}^{2}+1)}{(3{k}^{2}+1)^{2}}$,
=$\frac{3}{4}$,整理得:9k4-6k2+1=0,解得:k2=$\frac{1}{3}$,
∴k=±$\frac{\sqrt{3}}{3}$,
直线l的倾斜角$\frac{π}{6}$或$\frac{5π}{6}$.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,点到直线的距离公式,向量的坐标运算,考查计算能力,属于中档题.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案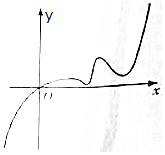 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
| A. | (0,2) | B. | (2,0) | C. | 2 | D. | 4 |
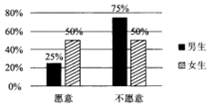 2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:
2017年1月1日,作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园,元旦期间,为了活跃气氛,主办方设置了水上挑战项目向全体市民开放,现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查,统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况,具体数据如图表:(1)根据条件完成下列2×2列联表,并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关?
| 愿意 | 不愿意 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 |
参考公式与数据:
| P(K2≥k0) | 0.1 | 0.05 | 0.025 | 0.01 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
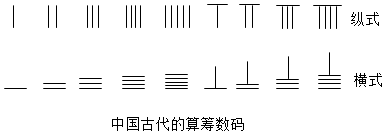
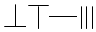 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )