题目内容
20．函数f（x）=x2-4x+4的零点是（ ）| A． | （0，2） | B． | （2，0） | C． | 2 | D． | 4 |
分析 由函数零点的定义列出方程x2-4x+4=0，求出方程的根是函数的零点．
解答 解：由f（x）=x2-4x+4=0得，x=2，
所以函数f（x）=x2-4x+4的零点是2，
故选C．
点评 本题考查函数零点的求法：定义法，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
11．四棱锥P-ABCD的底面ABCD是边长为6的正方形，且PA=PB=PC=PD，若一个半径为1的球与此四棱锥所有面都相切，则该四棱锥的高是（ ）
| A． | 6 | B． | 5 | C． | $\frac{9}{2}$ | D． | $\frac{9}{4}$ |
12．
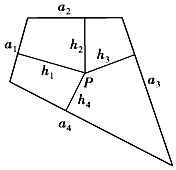如图所示，面积为S的平面凸四边形的第i条边的边长为ai（i=1，2，3，4），此四边形内在一点P到第i条边的距离记为hi（i=1，2，3，4），若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k，则h1+3h2+5h3+7h4=$\frac{2S}{k}$．类比以上性质，体积为V的三棱锥的第i个面的面积记为Si（i=1，2，3，4），此三棱锥内任一点Q到第i个面的距离记为Hi（i=1，2，3，4），若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K，H1+3H2+5H3+7H4=（ ）
如图所示，面积为S的平面凸四边形的第i条边的边长为ai（i=1，2，3，4），此四边形内在一点P到第i条边的距离记为hi（i=1，2，3，4），若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k，则h1+3h2+5h3+7h4=$\frac{2S}{k}$．类比以上性质，体积为V的三棱锥的第i个面的面积记为Si（i=1，2，3，4），此三棱锥内任一点Q到第i个面的距离记为Hi（i=1，2，3，4），若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K，H1+3H2+5H3+7H4=（ ）| A． | $\frac{V}{2K}$ | B． | $\frac{2V}{K}$ | C． | $\frac{3V}{K}$ | D． | $\frac{V}{3K}$ |
9．已知函数f（x）=$\left\{\begin{array}{l}{kx+3，x≥0}\\{（\frac{1}{2}）^{x}，x＜0}\end{array}\right.$，若方程f（f（x））-2=0恰有三个实数根，则实数k的取值范围是（ ）
| A． | [0，+∞） | B． | [1，3] | C． | （-1，-$\frac{1}{3}$] | D． | [-1，-$\frac{1}{3}$] |
10．
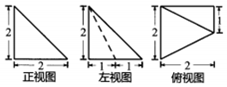某一空间几何体的三视图如图所示，则该几何体的最长棱长为（ ）
某一空间几何体的三视图如图所示，则该几何体的最长棱长为（ ）| A． | 2 | B． | $\sqrt{5}$ | C． | 2$\sqrt{2}$ | D． | 3 |