题目内容
10.已知定义在R上的函数满足f(x)=$\frac{f′(1)}{2}$•e2x-2+x2-2f(0)•x,则f′(1)=( )| A. | 2 | B. | e | C. | 3 | D. | 2e2 |
分析 求导数得到f′(x)=f′(1)e2x-2+2x-2f(0),代入x=1便可得出f(0)=1,而x=0代入f(x)即可得到$f(0)=\frac{f′(1)}{2}•{e}^{-2}$,这样即可求出f′(1)的值.
解答 解:f′(x)=f′(1)e2x-2+2x-2f(0);
∴f′(1)=f′(1)+2-2f(0);
∴f(0)=1;
又$f(0)=\frac{f′(1)}{2}•{e}^{-2}$;
即$1=\frac{f′(1)}{2}•{e}^{-2}$;
∴f′(1)=2e2.
故选D.
点评 考查复合函数的求导公式,以及基本初等函数的求导公式.

练习册系列答案
相关题目
5.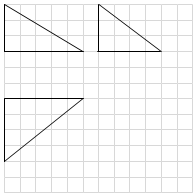 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O的球面上,则球O的表面积为( )| A. | 25π | B. | 50π | C. | 75π | D. | 100π |
2.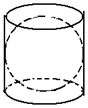 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
 如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )
如图所示,圆柱形容器的底面直径等于球的直径2R,把球放在在圆柱里,注入水,使水面与球正好相切,然后将球取出,此时容器中水的深度是( )| A. | 2R | B. | $\frac{4R}{3}$ | C. | $\frac{2}{3}R$ | D. | $\frac{R}{3}$ |
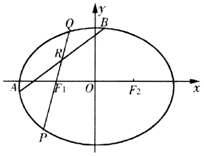 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$过点$({\sqrt{3},\frac{{\sqrt{3}}}{2}})$,左右焦点为F1(-c,0),F2(c,0),且椭圆C关于直线x=c对称的图形过坐标原点.