题目内容
6.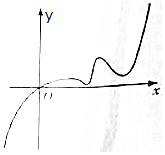 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
分析 由已知可得2a+b<2,又由a>0.b>0;画出满足约束条件的可行域,结合$\frac{b+2}{a+2}$的几何意义,可得答案.
解答 解:由图可知,当x>0时,导函数f'(x)>0,原函数单调递增,
∵两正数a,b满足f(2a+b)<2,
又由f(2)=2,即f(2a+b)<2,
即2a+b<2,
又由a>0.b>0;
故a,b所对应的平面区域如下图所示: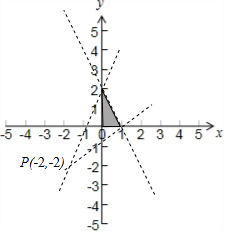
$\frac{b+2}{a+2}$表示动点(a,b)与定点(-2,-2)连线的斜率,
当直线过(1,0)点时,$\frac{b+2}{a+2}$=$\frac{2}{3}$,
当直线过(0,2)点时,$\frac{b+2}{a+2}$=2,
故$\frac{b+2}{a+2}$∈($\frac{2}{3}$,2),
故选:A.
点评 本题考查的知识点是利用导数研究函数的单调性,直线的斜率公式,线性规划的应用,难度中档.

练习册系列答案
相关题目
16.设袋中有两个红球一个黑球,除颜色不同,其他均相同,现有放回的抽取,每次抽取一个,记下颜色后放回袋中,连续摸三次,X表示三次中红球被摸中的次数,每个小球被抽取的几率相同,每次抽取相对立,则方差D(X)=( )
| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
11.四棱锥P-ABCD的底面ABCD是边长为6的正方形,且PA=PB=PC=PD,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是( )
| A. | 6 | B. | 5 | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
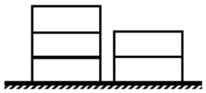 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是10(用数字作答).