题目内容
7．已知正三棱柱ABC-A1B1C1的顶点都在同一个球面上，且该正三棱柱的体积为$\frac{\sqrt{3}}{2}$，三角形ABC周长为3，则这个球的体积为$\frac{16π}{3}$．分析 正三棱柱的底面中心的连线的中点就是外接球的球心，求出球的半径即可求出球的表面积．
解答 解：由题意可知：$\frac{\sqrt{3}}{4}•1•$AA1=$\frac{\sqrt{3}}{2}$，∴AA1=2
正三棱柱的底面中心的连线的中点就是外接球的球心，底面中心到顶点的距离为：$\frac{\sqrt{3}}{3}$；
所以外接球的半径为：$\sqrt{\frac{1}{3}+1}$=$\sqrt{\frac{4}{3}}$．
所以外接球的表面积为：4π（$\sqrt{\frac{4}{3}}$）2=$\frac{16π}{3}$．
故答案为：$\frac{16π}{3}$．
点评 本题是中档题，考查正三棱柱的外接球的表面积的求法，找出球的球心是解题的关键，考查空间想象能力，计算能力．
练习册系列答案
相关题目
2．
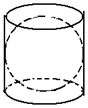如图所示，圆柱形容器的底面直径等于球的直径2R，把球放在在圆柱里，注入水，使水面与球正好相切，然后将球取出，此时容器中水的深度是（ ）
如图所示，圆柱形容器的底面直径等于球的直径2R，把球放在在圆柱里，注入水，使水面与球正好相切，然后将球取出，此时容器中水的深度是（ ）| A． | 2R | B． | $\frac{4R}{3}$ | C． | $\frac{2}{3}R$ | D． | $\frac{R}{3}$ |
12．
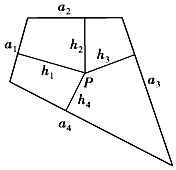如图所示，面积为S的平面凸四边形的第i条边的边长为ai（i=1，2，3，4），此四边形内在一点P到第i条边的距离记为hi（i=1，2，3，4），若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k，则h1+3h2+5h3+7h4=$\frac{2S}{k}$．类比以上性质，体积为V的三棱锥的第i个面的面积记为Si（i=1，2，3，4），此三棱锥内任一点Q到第i个面的距离记为Hi（i=1，2，3，4），若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K，H1+3H2+5H3+7H4=（ ）
如图所示，面积为S的平面凸四边形的第i条边的边长为ai（i=1，2，3，4），此四边形内在一点P到第i条边的距离记为hi（i=1，2，3，4），若$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k，则h1+3h2+5h3+7h4=$\frac{2S}{k}$．类比以上性质，体积为V的三棱锥的第i个面的面积记为Si（i=1，2，3，4），此三棱锥内任一点Q到第i个面的距离记为Hi（i=1，2，3，4），若$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K，H1+3H2+5H3+7H4=（ ）| A． | $\frac{V}{2K}$ | B． | $\frac{2V}{K}$ | C． | $\frac{3V}{K}$ | D． | $\frac{V}{3K}$ |
17．如图为某几何体的三视图，则其体积为（ ）
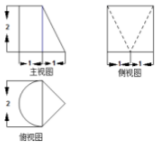
| A． | π+$\frac{4}{3}$ | B． | $\frac{π}{3}$+4 | C． | $\frac{2}{3}$π+$\frac{4}{3}$ | D． | $\frac{2}{3}$π+4 |