��Ŀ����
4����֪ai��0��i=1��2��3������n�����۲����в���ʽ��$\frac{{{a_1}+{a_2}}}{2}��\sqrt{{a_1}{a_2}}$��$\frac{{{a_1}+{a_2}+{a_3}}}{3}��\root{3}{{{a_1}{a_2}{a_3}}}$��$\frac{{{a_1}+{a_2}+{a_3}+{a_4}}}{4}��\root{4}{{{a_1}{a_2}{a_3}{a_4}}}$����
�մ˹��ɣ���n��N*��n��2��ʱ��$\frac{{{a_1}+{a_2}+��+{a_n}}}{n}��$$\root{n}{{{a_1}{a_2}��{a_n}}}$��
���� �����⣬֪���ÿһ��ʽ��������ƽ�������ұߵ�ʽ���Ǽ���ƽ������������������ƽ������С�����ǵļ���ƽ���������ɵó����ۣ�
��� �⣺�����⣬֪���ÿһ��ʽ��������ƽ�������ұߵ�ʽ���Ǽ���ƽ������������������ƽ������С�����ǵļ���ƽ������
�����Ʋn��N*��n��2��ʱ��$\frac{{{a_1}+{a_2}+��+{a_n}}}{n}��$$\root{n}{{{a_1}{a_2}��{a_n}}}$��
�ʴ�Ϊ��$\root{n}{{{a_1}{a_2}��{a_n}}}$��
���� ���⿼���������������ѧ���������������������Ƚϻ�����

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
12��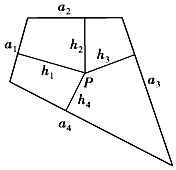 ��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������
��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������
 ��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������
��ͼ��ʾ�����ΪS��ƽ���ı��εĵ�i���ߵı߳�Ϊai��i=1��2��3��4�������ı�������һ��P����i���ߵľ����Ϊhi��i=1��2��3��4������$\frac{a_1}{1}=\frac{a_2}{3}=\frac{a_3}{5}=\frac{a_4}{7}$=k����h1+3h2+5h3+7h4=$\frac{2S}{k}$������������ʣ����ΪV�������ĵ�i����������ΪSi��i=1��2��3��4��������������һ��Q����i����ľ����ΪHi��i=1��2��3��4������$\frac{S_1}{1}=\frac{S_2}{3}=\frac{S_3}{5}=\frac{S_4}{7}$=K��H1+3H2+5H3+7H4=��������| A�� | $\frac{V}{2K}$ | B�� | $\frac{2V}{K}$ | C�� | $\frac{3V}{K}$ | D�� | $\frac{V}{3K}$ |
9����֪����f��x��=$\left\{\begin{array}{l}{kx+3��x��0}\\{��\frac{1}{2}��^{x}��x��0}\end{array}\right.$��������f��f��x����-2=0ǡ������ʵ��������ʵ��k��ȡֵ��Χ�ǣ�������
| A�� | [0��+�ޣ� | B�� | [1��3] | C�� | ��-1��-$\frac{1}{3}$] | D�� | [-1��-$\frac{1}{3}$] |
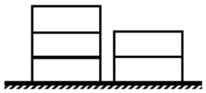 ��ͼ��ʾ��ij���������Ѽ�װ�䣬һ��2����һ��3��������Ҫȫ��װ�ˣ�ÿ��ֻ�ܴ�����һ��ȡ�������һ����װ�䣬����װ�˵Ĺ����в�ͬȡ����������10�����������𣩣�
��ͼ��ʾ��ij���������Ѽ�װ�䣬һ��2����һ��3��������Ҫȫ��װ�ˣ�ÿ��ֻ�ܴ�����һ��ȡ�������һ����װ�䣬����װ�˵Ĺ����в�ͬȡ����������10�����������𣩣� �й��ļ�����λ�����ݵ�4000����ǰ���������ĩ�ڣ���Ԫǰ221�꣬����ͳһ�й��䲼ͬһ�������گ�鲢�Ʒ��˳���Ȩ���������������ͼ�ǹŴ���һ�ֶ������ߡ��������ǣ���������ȣ�������ͼ��������ͼ�Ͳ���ͼΪ�������Σ�����ˡ����������Ϊ����λ���������ף���������
�й��ļ�����λ�����ݵ�4000����ǰ���������ĩ�ڣ���Ԫǰ221�꣬����ͳһ�й��䲼ͬһ�������گ�鲢�Ʒ��˳���Ȩ���������������ͼ�ǹŴ���һ�ֶ������ߡ��������ǣ���������ȣ�������ͼ��������ͼ�Ͳ���ͼΪ�������Σ�����ˡ����������Ϊ����λ���������ף��������� ��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮
��֪��ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������㣨$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{3}}{2}$����������Ϊ$\frac{2\sqrt{5}}{5}$����Oλ����ԭ�㣮