题目内容
设函数f(x)=sin(wx+θ)(-π<θ<0),y=f(x),周期为π,图象的一个对称中心为(
,0)
(1)求f(x)的解析式
(2)求函数y=f(x)的单调增区间
(3)在△ABC中,a,b,c分别为A,B,C的对边,S为其面积,若f(
)=0,b=1,S△ABC=
,求a的值.
| π |
| 6 |
(1)求f(x)的解析式
(2)求函数y=f(x)的单调增区间
(3)在△ABC中,a,b,c分别为A,B,C的对边,S为其面积,若f(
| A |
| 2 |
| ||
| 2 |
考点:正弦函数的图象
专题:三角函数的图像与性质,解三角形
分析:(1)由周期为π,可求得ω=2,由图象的一个对称中心为(
,0),可解得θ=-
.从而可求得f(x)的解析式为:f(x)=sin(2x-
);
(2)由2kπ-
≤2x-
≤2kπ+
,k∈Z可解得函数y=f(x)的单调增区间为:[kπ-
,kπ+
],k∈Z.
(3)由f(
)=0可求得A=
,由b=1,S△ABC=
bcsinA=
c×
=
,解得c=2,从而由余弦定理知a2=b2+c2-2bccosA=3,即可求得a的值.
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
(3)由f(
| A |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:(1)∵周期为π,∴T=
=π,∴ω=2.
∵图象的一个对称中心为(
,0),∴0=sin(2×
+θ),-π<θ<0,∴可解得θ=-
.
∴f(x)的解析式为:f(x)=sin(2x-
)
(2)由2kπ-
≤2x-
≤2kπ+
,k∈Z可解得kπ-
≤x≤kπ+
,故函数y=f(x)的单调增区间为:[kπ-
,kπ+
],k∈Z.
(3)∵f(
)=0,∴sin(A-
)=0,解得sinA=
cosA,从而有tanA=
,A为△ABC中的内角,故A=
.
∵b=1,有S△ABC=
bcsinA=
c×
=
,解得c=2.
∴由余弦定理知:a2=b2+c2-2bccosA=1+4-2×1×2×
=3.
故求得:a=
.
| 2π |
| ω |
∵图象的一个对称中心为(
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∴f(x)的解析式为:f(x)=sin(2x-
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
(3)∵f(
| A |
| 2 |
| π |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
∵b=1,有S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴由余弦定理知:a2=b2+c2-2bccosA=1+4-2×1×2×
| 1 |
| 2 |
故求得:a=
| 3 |
点评:本题主要考查了正弦函数的图象和性质,考查了余弦定理的应用,属于基本知识的考查.

练习册系列答案
相关题目
连续抛掷一枚硬币3次,则至少有一次正面向上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线l、m、n与平面α、β,给出下列四个命题:
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
①若m∥l,n∥l,则m∥n;
②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;
④若m⊥β,α⊥β,则m∥α;
其中假命题是( )
| A、① | B、② | C、③ | D、③④ |
若实数x、y满足
,则S=2x+y的最大值为( )
|
| A、3 | B、2 | C、6 | D、7 |
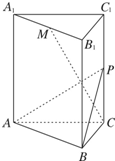 如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2
如图,三棱柱ABC-A1B1C1的底面是边长为4正三角形,AA1⊥平面ABC,AA1=2