Question

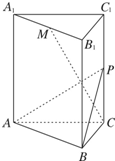如图，三棱柱ABC-A₁B₁C₁的底面是边长为4正三角形，AA₁⊥平面ABC，AA₁=2

6

，M为A₁B₁的中点．
（Ⅰ）求证：MC⊥AB；
（Ⅱ）求三棱锥A₁-ABP的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面垂直的性质

专题：空间位置关系与距离

分析：（Ⅰ）通过证明AB⊥平面OMC，然后利用直线与平面垂直的性质定理证明MC⊥AB；
（Ⅱ）转化三棱锥A₁-ABP的体积为三棱锥P-A₁AB的体积，利用已知条件求解即可．

解答： （本小题满分12分）
解：（I）取AB中点O，连接OM，OC．
∵M为A₁B₁中点，∴MO∥A₁A，又A₁A⊥平面ABC，∴MO⊥平面ABC，
∴MO⊥AB…（2分）
∵△ABC为正三角形，∴AB⊥CO  又MO∩CO=O，∴AB⊥平面OMC
又∵MC?平面OMC∴AB⊥MC…（5分）
（Ⅱ）如图，VA1-ABP=VP-A1BA=

1

3

S△A1BA•d=

1

3

×

1

2

AB•AA1•CO
=

1

3

×

1

2

×4×2

6

×2

3

=8

2

．

点评：本题考查棱锥的体积的求法，直线与平面垂直的性质定理的应用，考查空间想象能力以及转化思想．